|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
II Звезды излучают ...Так продолжал я передвигаться по времени огромными шагами, каждый в тысячу лет и больше, увлекаемый тайной последних дней Земли и наблюдая в состоянии какого-то гипноза, как в западной части неба Солнце становится все огромнее и тусклее... Наконец, больше чем через тридцать миллионов лет огромный красный купол Солнца заслонил собой десятую часть потемневших небес... (Г. Уэллс, «Машина Времени» — гениальное предвидение в 1895 году, еще до открытия законов излучения, стадии красного гиганта как заключительного этапа эволюции Солнца) Глава 6 Звезда — газовый шар, находящийся в состоянии равновесия Представляется почти очевидным тот факт, что подавляющее большинство звезд не меняет своих свойств в течение огромных промежутков времени. Это утверждение совершенно очевидно для интервала времени по крайней мере в 60 лет, в течение которых астрономы разных стран выполнили очень большую работу, по измерению блеска, цвета и спектра множества звезд. Заметим что хотя некоторые звезды меняют свои характеристики (такие звезды называются переменными; см. § 1), изменения носят либо строго периодический либо более или менее периодический характер. Систематические изменения блеска, спектра или цвета у звезд наблюдаются в очень редких случаях. Например, изменения периодов пульсирующих звезд-цефеид хотя и обнаружены, но они настолько малы, что требуется по крайней мере несколько миллионов лет для того, чтобы изменения периода пульсаций стали значительными. С другой стороны, мы знаем (см. § 1), что светимость цефеид меняется с изменением периода. Можно, следовательно, сделать вывод, что в течение по крайней мере нескольких миллионов лет у таких звезд их важнейшая характеристика — мощность излучаемой энергии — меняется мало. На этом примере мы видим, что хотя длительность наблюдений составляет всего лишь несколько десятков лет (срок совершенно ничтожный по космическим масштабам!), можно сделать вывод о постоянстве свойств цефеид в течение неизмеримо больших интервалов времени. Но в нашем распоряжении есть еще одна возможность оценить время, в течение которого мощность излучения звезд почти не меняется. Из геологических данных следует, что на протяжении по крайней мере последних двух-трех миллиардов лет температура Земли если и менялась, то не больше, чем на несколько десятков градусов. Это следует из непрерывности эволюции жизни на Земле. А если так, то Солнце за этот огромный промежуток времени никогда не излучало ни в три раза сильнее, ни в три раза слабее, чем сейчас. Похоже на то, что в столь длительной истории нашего светила были периоды, когда его излучение значительно (но не очень сильно) отличалось от нынешнего уровня, но такие эпохи были сравнительно кратковременными. Мы имеем в виду ледниковые периоды, о которых речь будет идти в § 9. Но в среднем мощность излучения Солнца за последние несколько миллиардов лет отличалась удивительным постоянством. В то же время Солнце — довольно типичная звезда. Как мы знаем (см. § 1), оно представляет собой желтый карлик спектрального класса G2. Таких звезд в нашей Галактике насчитывается по крайней мере несколько миллиардов. Вполне логично также сделать вывод, что и большинство других звезд главной последовательности, у которых спектральные классы отличны от солнечного, также должны быть весьма «долгоживущими» объектами. Итак, подавляющее большинство звезд очень мало меняется со временем. Это, конечно, не означает, что они в «неизменном виде» могут существовать сколь угодно долго. Наоборот, ниже мы покажем, что возраст звезд хотя и очень велик, но конечен. Более того, этот возраст весьма различен для разных звезд и определяется в первую очередь их массой. Но даже самые «короткоживущие» звезды все-таки почти не меняют своих характеристик в течение миллиона лет. Какие же выводы отсюда следуют? Уже из простейшего анализа спектров звезд вытекает, что их наружные слои должны находиться в газообразном состоянии. В противном случае, очевидно, в этих спектрах никогда не наблюдались бы резкие линии поглощения, характерные для вещества, находящегося в газообразном состоянии. Дальнейший анализ звездных спектров позволяет существенно уточнить свойства вещества наружных слоев звезд (т. е. «звездных атмосфер»), откуда к нам приходит их излучение. Изучение спектров звезд позволяет с полной достоверностью сделать вывод, что звездные атмосферы представляют собой нагретый до температуры в тысячи и десятки тысяч градусов ионизованный газ, т. е. плазму. Спектральный анализ позволяет определить химический состав звездных атмосфер, который в большинстве случаев примерно такой же, как и у Солнца. Наконец, изучая звездные спектры, можно определить и плотность звездных атмосфер, которая для различных звезд меняется в очень широких пределах. Итак, наружные слои звезд — это газ. Но в этих слоях заключена ничтожно малая доля массы всей звезды. Хотя непосредственно оптическими методами недра звезд из-за их огромной непрозрачности наблюдать нельзя, мы можем сейчас со всей определенностью утверждать, что и внутренние слои звезд также находятся в газообразном состоянии. Это утверждение отнюдь не является очевидным. Например, поделив массу Солнца, равную 2 Итак, звезды — это огромные газовые шары. Весьма существенно, что такой газовый шар «цементируется» силой всемирного тяготения, т. е. гравитацией. На каждый элемент объема звезды действует сила гравитационного притяжения от всех остальных элементов звезды. Именно эта сила препятствует разлету различных частей газа, образующего звезду, в окружающее пространство. Если бы не было этой силы, газ, образующий звезду, вначале расплылся бы, образовав нечто вроде плотной туманности, а потом окончательно рассеялся бы в огромном, окружающем звезду межзвездном пространстве. Сделаем очень грубую оценку, сколько бы потребовалось времени, чтобы при таком «расплывании» размер звезды увеличился бы, скажем, в 10 раз. Примем, что «расплывание» происходит с тепловой скоростью атомов водорода (из которого в основном состоит звезда) при температуре наружных слоев звезды, т. е. около 10 000 К. Эта скорость близка к 10 км/с, т. е. 106 см/с. Так как радиус звезды можно принять близким к миллиону километров (т. е. 1011 см), то для интересующего нас «расплывания» с десятикратным увеличением размеров звезды потребуется ничтожно малое время t = 10 Это означает, что если бы не сила гравитационного притяжения, звезды рассеялись бы в окружающем пространстве за ничтожно малое (по астрономическим понятиям) время, исчисляемое сутками для звезд-карликов или годами для гигантов. Значит, без силы всемирного тяготения не было бы звезд. Действуя непрерывно, эта сила стремится сблизить между собой различные элементы звезды. Очень важно подчеркнуть, что сила гравитации по самой своей природе стремится неограниченно сблизить между собой все частицы звезды, т. е. в пределе как бы «собрать всю звезду в точку». Но если бы на частицы, образующие звезду, действовала только сила всемирного тяготения, то звезда стала бы катастрофически быстро сжиматься. Оценим сейчас время, в течение которого это сжатие станет существенным. Если бы никакая сила не противодействовала гравитации, вещество звезды падало бы по направлению к ее центру по законам свободного падения тел. Рассмотрим элемент вещества внутри звезды где-нибудь между ее поверхностью и центром на расстоянии R от последнего. На этот элемент действует ускорение силы тяготения g =
где t — время падения, причем мы положили R Какая же сила, непрерывно действующая во всем объеме звезды, противодействует силе гравитации? Заметим, что в каждом элементарном объеме звезды направление этой силы должно быть противоположно, а величина равна силе притяжения. В противном случае происходили бы локальные, местные нарушения равновесия, приводившие за очень короткое время, которое мы только что оценили, к большим изменениям в структуре звезды. Силой, противодействующей гравитации, является давление газа[ 16 ]. Последнее непрерывно стремится расширить звезду, «рассеять» ее на возможно больший объем. Выше мы уже оценили, как быстро «рассеялась» бы звезда, если бы отдельные ее части не сдерживались силой гравитации. Итак, из того простого факта, что звезды — газовые шары в практически неизменном виде (т. е. не сжимаясь и не расширяясь) существуют по меньшей мере миллионы лет, следует, что каждый элемент вещества звезды находится в равновесии под действием противоположно направленных сил гравитации и газового давления. Такое равновесие называется «гидростатическим». Оно широко распространено в природе. В частности, земная атмосфера находится в гидростатическом равновесии под действием силы гравитационного притяжения Земли и давления находящихся в ней газов. Если бы не было давления, земная атмосфера очень быстро «упала» бы на поверхность нашей планеты. Следует подчеркнуть, что гидростатическое равновесие в звездных атмосферах осуществляется с огромной точностью. Малейшее его нарушение сразу же приводит к появлению сил, меняющих распределение вещества в звезде, после чего происходит такое его перераспределение, при котором равновесие восстанавливается. Здесь мы всегда говорим об обычных «нормальных» звездах. В исключительных случаях, о которых в этой книге будет идти речь, нарушение равновесия между силой гравитации и давлением газа приведет к весьма серьезным, даже катастрофическим последствиям в жизни звезды. А сейчас мы можем только сказать, что история существования любой звезды — это поистине титаническая борьба между силой гравитации, стремящейся ее неограниченно сжать, и силой газового давления, стремящейся ее «распылить», рассеять в окружающем межзвездном пространстве. Многие миллионы и миллиарды лет длится эта «борьба». В течение этих чудовищно больших сроков силы равны. Но в конце концов, как мы увидим дальше, победа будет за гравитацией. Такова драма эволюции любой звезды. Ниже мы будем довольно подробно останавливаться на отдельных этапах этой драмы, связанных с финальными стадиями эволюции звезд. В центральной части «нормальной» звезды вес вещества, заключенного в столбе, площадь основания которого равна одному квадратному сантиметру, а высота — радиусу звезды, будет равен давлению газа у основания столба. С другой стороны, масса столба равна силе, с которой он притягивается к центру звезды. Мы сейчас проведем весьма упрощенный расчет, который, тем не менее, вполне отражает существо вопроса. А именно, положим массу нашего столба M1 =
Сделаем теперь оценку величины газового давления P в центральной части такой звезды, какой является наше Солнце. Подставив численное значение величин, стоящих в правой части этого уравнения, найдем, что P = 1016 дин/см2, или 10 миллиардов атмосфер! Это неслыханно большая величина. Самое высокое «стационарное» давление, достигаемое в земных лабораториях, порядка нескольких миллионов атмосфер[ 17 ]. Из элементарного курса физики известно, что давление газа зависит от его плотности В формулу Клапейрона входит также средняя молекулярная масса
Величина При температуре порядка десяти миллионов кельвинов и при плотностях, которые там существуют, все атомы должны быть ионизованы. В самом деле, средняя кинетическая энергия каждой частицы газа Это означает, что каждое столкновение электрона с атомом может привести к ионизации последнего, так как энергия связи электронов в атоме (так называемый «потенциал ионизации»), как правило, меньше тысячи электронвольт. Только самые «глубокие» электронные оболочки у тяжелых атомов останутся «нетронутыми», т. е. будут удержаны своими атомами. Состояние ионизации внутри-звездного вещества определяет его среднюю молекулярную массу, величина которой, как мы уже имели возможность убедиться, играет большую роль в недрах звезд. Если бы вещество звезды состояло только из полностью ионизованного водорода (как мы положили выше), то средняя молекулярная масса В действительности вещество звездных недр представляет собой некоторую смесь водорода, гелия и тяжелых элементов. Относительное содержание этих основных компонент звездного вещества (не по числу атомов, а по массе) обычно обозначается через буквы X, Y и Z, которые характеризуют химический состав звезды. У типичных звезд, более или менее сходных с Солнцем, X = 0,73, Y = 0,25, Z = 0,02. Отношение Y/X
Роль Z в оценке
где T Существенно, что температура Глава 7 Как излучают звезды? При температуре порядка десяти миллионов кельвинов и достаточно высокой плотности вещества недра звезды должны быть «наполнены» огромным количеством излучения. Кванты этого излучения непрерывно взаимодействуют с веществом, поглощаясь и переизлучаясь им. В результате таких процессов поле излучения приобретает равновесный характер (строго говоря, почти равновесный характер — см. ниже), т. е. оно описывается известной формулой Планка с параметром T, равным температуре среды. Например, плотность излучения на частоте
в то время как полная плотность излучения задается известным законом Стефана — Больцмана
Важной характеристикой поля излучения является его интенсивность, обычно обозначаемая символом I
Аналогично, полная интенсивность I связана с плотностью излучения и выражением
Наконец, особое значение для проблемы внутреннего строения звезд имеет поток излучения, обозначаемый буквой H. Мы можем определить эту важную величину через полное количество энергии, протекающей наружу через некоторую воображаемую сферу, окружающую центр звезды:
Если энергия «производится» только в самых внутренних областях звезды, то величина L остается постоянной, т. е. не зависит от произвольно выбранного радиуса r. Полагая r = R, т. е. радиусу звезды, мы найдем смысл L: очевидно, это просто светимость звезды. Что же касается величины потока H, то она меняется с глубиной как r-2. Если бы интенсивность излучения по всем направлениям была строго одинакова (т. е., как говорят, поле излучения было бы изотропным), то поток H был бы равен нулю[ 18 ]. Это легко понять, если представить, что в изотропном поле количество излучения, вытекающее через сферу произвольного радиуса наружу, равно количеству втекающей внутрь этой воображаемой сферы энергии. В условиях звездных недр поле излучения почти изотропно. Это означает, что величина I подавляюще превосходит H. В этом мы можем убедиться непосредственно. Согласно (7.2) и (7.4) при T = 107 К I = 1023 эрг/см2 При T
где Возникает основной вопрос: чем определяется светимость звезды, т. е. мощность ее излучения? Почему звезда, имеющая огромные ресурсы энергии, так «экономно» расходует их, теряя из этого «запаса» на излучение лишь малую, хотя и вполне определенную часть? Выше мы оценили запас лучистой энергии в недрах звезд. Следует иметь в виду, что эта энергия, взаимодействуя с веществом, непрерывно поглощается и в таком же количестве возобновляется. «Резервуаром» для «наличной» лучистой энергии в недрах звезд служит тепловая энергия частиц вещества. Не представляет особого труда оценить величину тепловой энергии, запасенной в звезде. Для определенности рассмотрим Солнце. Считая, для простоты, что оно состоит только из водорода, и зная его массу, легко найти, что там имеется приблизительно 2
где Te — температура солнечной поверхности[ 19 ]. Ведь, в принципе, Солнце при тех же массе и радиусе могло бы иметь температуру, скажем, 20 000 К, и тогда его светимость была бы в сотни раз больше. Однако этого нет, что, конечно, не является случайностью. Выше мы говорили о запасе тепловой энергии в звезде. Наряду с тепловой энергией звезда располагает также солидным запасом других видов энергии. Прежде всего рассмотрим гравитационную энергию. Последняя определяется как энергия гравитационного притяжения всех частиц звезды между собой. Она, конечно, является потенциальной энергией звезды и имеет знак минус. Численно она равна работе, которую нужно затратить, чтобы, преодолевая силу тяготения, «растащить» все части звезды на бесконечно большое расстояние от ее центра. Оценку величины этой энергии можно сделать, если найти энергию гравитационного взаимодействия звезды с самой собой:
Точный расчет с использованием простых методов высшей математики дает примерно вдвое большее значение, причем строго выполняется соотношение, известное в механике как «теорема о вириале»:
Рассмотрим теперь звезду не в равновесном, стационарном состоянии, а в стадии медленного сжатия (как это имеет место для протозвезды; см. § 5). В процессе сжатия гравитационная энергия звезды медленно уменьшается (вспомним, что она отрицательна). Однако, как это видно из формулы (7.9), только половина выделившейся гравитационной энергии перейдет в тепло, т. е. будет затрачена на нагрев вещества. Другая половина выделившейся энергии обязательно должна покинуть звезду в виде излучения. Отсюда следует, что если источником энергии излучения звезды является ее сжатие, то количество излученной за время эволюции энергии равно запасу ее тепловой энергии. Оставляя пока в стороне очень важный вопрос о причинах, по которым звезда имеет совершенно определенную светимость, сразу же подчеркнем, что если считать источником энергии звезды освобождение ее гравитационной энергии в процессе сжатия (как это полагали в конце XIX века), то мы столкнемся с очень серьезными трудностями. Дело не в том, что для обеспечения наблюдаемой светимости радиус Солнца ежегодно должен уменьшаться примерно на 20 метров — такое ничтожное изменение размеров Солнца современная техника наблюдательной астрономии обнаружить не в состоянии. Трудность в том, что запаса гравитационной энергии Солнца хватило бы лишь на 30 миллионов лет излучения нашего светила при условии, конечно, что оно излучало в прошлом примерно так же, как сейчас. Если в XIX веке, когда известный английский физик Томпсон (лорд Кельвин) выдвинул эту «гравитационную» гипотезу поддержания солнечного излучения, знания о возрасте Земли и Солнца были весьма туманными, то сейчас это уже не так. Геологические данные с большой надежностью позволяют утверждать, что возраст Солнца исчисляется по крайней мере в несколько миллиардов лет, что в сотню раз превышает «кельвинскую шкалу» для его жизни. Отсюда следует очень важный вывод, что ни тепловая, ни гравитационная энергия не могут обеспечить столь длительное излучение Солнца, а также подавляющего большинства других звезд. Наш век уже давно указал на третий источник энергии излучения Солнца и звезд, имеющий решающее значение для всей нашей проблемы. Речь идет о ядерной энергии (см. § 3). В § 8 мы более подробно и конкретно будем говорить о тех ядерных реакциях, которые протекают в звездных недрах. Величина запаса ядерной энергии Wя = 0,008Xc2M Важно подчеркнуть, что ядерные реакции, происходящие в недрах Солнца и звезд, являются термоядерными. Это означает, что реагируют хотя и быстрые (а поэтому достаточно энергичные) заряженные частицы, но все же тепловые. Дело в том, что частицы газа, нагретого до некоторой температуры, имеют максвеллово распределение скоростей. При температуре Таким образом, скорость ядерных реакций как бы «подстраивается» к распределению температуры внутри звезды. Как это ни звучит парадоксально, величина светимости звезды не зависит от ядерных реакций, происходящих в ее недрах! Значение ядерных реакций состоит в том, что они как бы поддерживают установившийся температурный режим на том уровне, который определяется структурой звезды, обеспечивая светимость звезд в течение «космогонических» интервалов времени. Таким образом, «нормальная» звезда (например, Солнце) является великолепно отрегулированной машиной, которая может в течение огромного времени работать в стабильном режиме. Теперь мы должны подойти к ответу на тот основной вопрос, который был поставлен в начале этого параграфа: если светимость звезды не зависит от находящихся в ней источников энергии, то чем же она определяется? Чтобы ответить на этот вопрос, надо прежде всего понять, каким образом в недрах звезд осуществляется транспортировка (перенос) энергии от центральных частей к периферии. Известны три основных способа переноса энергии: а) теплопроводность, б) конвекция, в) лучеиспускание. У большинства звезд, в том числе и у Солнца, механизм переноса энергии путем теплопроводности оказывается совершенно не эффективным по сравнению с другими механизмами. Исключение составляют недра белых карликов, о которых речь будет идти в § 10. Конвекция имеет место тогда, когда тепловая энергия переносится вместе с веществом. Например, соприкасающийся с горячей поверхностью нагретый газ расширяется, от этого его плотность уменьшается и он удаляется от нагревающего тела — просто «всплывает». На его место опускается холодный газ, который опять нагревается и всплывает, и т. д. Такой процесс может при некоторых условиях происходить довольно бурно. Его роль в самых центральных областях сравнительно массивных звезд, а также в их наружных, «подфотосферных» слоях может быть весьма значительной, о чем речь пойдет ниже. Основным процессом переноса энергии в звездных недрах является все же лучеиспускание. Мы уже говорили выше, что поле излучения в звездных недрах почти изотропно. Если мы вообразим себе малый объем звездного вещества где-нибудь в недрах звезды, то интенсивность излучения, идущего «снизу», т. е. по направлению от центра звезды, будет чуть-чуть больше, чем из противоположного направления. Именно по этой причине внутри звезды имеется поток излучения. От чего зависит разность интенсивностей излучения, идущего «сверху» и «снизу», т. е. поток излучения? Вообразим на минуту, что вещество звездных недр почти прозрачно. Тогда через наш объем «снизу» будет проходить излучение, которое возникло далеко от него, где-то в самой центральной области звезды. Так как температура там высока, то и интенсивность будет весьма значительной. Наоборот, интенсивность, идущая «сверху», будет соответствовать сравнительно низкой температуре наружных слоев звезды. В этом воображаемом случае разность интенсивностей излучения «снизу» и «сверху» будет весьма велика и ей будет соответствовать огромный поток излучения. Теперь представим себе другую крайность: вещество звезды очень непрозрачно. Тогда из данного объема можно «видеть» только на расстояние порядка l/ Таким образом, мы приходим к важному выводу, что непрозрачность звездного вещества определяет проходящий через него поток излучения, а следовательно, светимость звезды. Чем больше непрозрачность звездного вещества, тем меньше поток излучения. Кроме того, поток излучения должен, конечно, еще зависеть от того, как быстро меняется температура звезды с глубиной. Вообразим себе нагретый газовый шар, температура которого строго постоянна. Совершенно очевидно, что в этом случае поток излучения был бы равен нулю безотносительно к тому, велико или мало поглощение излучения. Ведь при любом Теперь мы вполне можем понять смысл точной формулы, связывающей светимость звезды с основными ее характеристиками:
где символ Формула (7.10) позволяет прежде всего получить, светимость звезды, если основные ее характеристики известны. Но прежде чем перейти к численным оценкам, мы эту формулу преобразуем. Выразим T через M, используя формулу (6.2), и примем, что Тогда, полагая
Характерной особенностью полученной формулы является то, что из нее выпала зависимость светимости от радиуса звезды. Хотя зависимость от среднего молекулярного веса вещества звездных недр довольно сильная, сама величина Теория приводит к простой зависимости коэффициента поглощения от характеристик вещества (формула Крамерса):
Заметим, однако, что эта формула носит довольно приближенный характер. Все же из нее следует, что мы не сделаем очень большой ошибки, если положим величину
Эта формула дает возможность определить абсолютное значение светимости звезды, если известна ее масса. Например, для Солнца можно принять, что коэффициент поглощения Основной смысл формулы (7.13) состоит в том, что она дает зависимость светимости звезды главной последовательности от ее массы. Поэтому формула (7.13) обычно называется «зависимость масса — светимость». Еще раз обратим внимание на то, что такая важнейшая характеристика звезды, как ее радиус, в эту формулу не входит. Нет и намека на зависимость светимости звезды от мощности источников энергии в ее недрах. Последнее обстоятельство имеет принципиальное значение. Как мы уже подчеркивали выше, звезда данной массы как бы сама регулирует мощность источников энергии, .которые «подстраиваются» под ее структуру и «непрозрачность». Зависимость «масса — светимость» была выведена впервые выдающимся английским астрономом Эддингтоном, основоположником современных теорий внутреннего строения звезд. Эта зависимость была найдена им теоретически и только впоследствии была подтверждена на обширном наблюдательном материале. Согласие этой формулы, полученной, как мы видели выше, из самых простых предположений, с результатами наблюдений в основном хорошее. Некоторые расхождения имеют место для очень больших и очень малых звездных масс (т. е. для голубых гигантов и красных карликов). Однако дальнейшее усовершенствование теории позволило эти расхождения устранить... Выше мы привели зависимость между потоком излучения и перепадом температуры, исходя из предположения, что энергия переносится из недр звезды наружу только путем лучеиспускания (см. формулу (7.10)). В недрах звезд при этом выполняется условие лучистого равновесия. Это означает, что каждый элемент объема звезды поглощает ровно столько энергии, сколько излучает. Однако такое равновесие не всегда является устойчивым. Поясним это на простом примере. Выделим небольшой элемент объема внутри звезды и мысленно перенесем его вверх (т. е. ближе к поверхности) на небольшое расстояние. Так как по мере удаления от центра звезды и температура и давление образующего его газа будут уменьшаться, наш объем при таком перемещении должен расшириться. Можно считать, что в процессе такого перемещения между нашим объемом и окружающей средой не происходит обмена энергии. Другими словами, расширение объема по мере его перемещения вверх можно считать адиабатическим. Это расширение будет происходить таким образом, что его внутреннее давление все время будет равно внешнему давлению окружающей среды. Если мы, после перемещения, представим наш объем газа «самому себе», то он либо вернется обратно в первоначальное положение, либо будет продолжать двигаться вверх. От чего же зависит направление движения объема?
На рис. 7.1 приведена схема, иллюстрирующая нашу задачу с объемом газа. Значение характеристик объема и окружающей среды в первоначальном состоянии обозначим индексом «1», а в конечном — индексом «2». Характеристики объема отметим звездочкой. Так как первоначальные характеристики объема совершенно не отличались от характеристик окружающей среды, то будут иметь место равенства
где
где В недрах звезд, как правило, перенос энергии осуществляется посредством лучеиспускания. Это объясняется устойчивостью среды по отношению к возмущениям ее «неподвижности» (см. выше). Но есть в недрах ряда звезд такие слои и даже целые большие области, где условие устойчивости, которое было получено выше, не выполняется. В этих случаях основная часть энергии переносится путем конвекции. Обычно это бывает тогда, когда перенос энергии путем лучеиспускания по каким-либо причинам оказывается ограниченным. Это может произойти, например» при слишком большой непрозрачности. Выше было получено основное соотношение «масса — светимость» из предположения, что перенос энергии в звездах осуществляется только путем лучеиспускания. Возникает вопрос: если в звезде имеет место также перенос энергии путем конвекции, не нарушится ли эта зависимость? Оказывается, нет! Дело в том, что «полностью конвективных звезд», т. е. таких звезд, у которых повсеместно, от центра до поверхности, перенос энергии осуществлялся бы только путем конвекции, в природе не существует. У реальных звезд имеются либо лишь более или менее тонкие слои, либо большие области в центре, где конвекция играет доминирующую роль. Но достаточно иметь хотя бы даже один слой внутри звезды, где бы перенос энергии осуществлялся лучеиспусканием, чтобы его непрозрачность самым радикальным образом отразилась бы на «пропускной способности» звезды по отношению к выделяющейся в ее недрах энергии. Однако наличие конвективных областей в недрах звезд, конечно, изменит численное значение коэффициентов в формуле (7.13). Это обстоятельство, в частности, является одной из причин, почему вычисленная нами по этой формуле светимость Солнца почти в пять раз превышает наблюдаемую. Итак, по причине описанной выше специфической неустойчивости, в конвективных слоях звезд происходят крупномасштабные движения газа. Более нагретые массы газа подымаются снизу вверх, в то время как более холодные опускаются. Происходит интенсивный процесс перемешивания вещества. Расчеты показывают, однако, что разница в температуре движущихся элементов газа и окружающей среды совершенно ничтожна, всего лишь около 1 К — и это при температуре вещества недр порядка десяти миллионов кельвинов! Это объясняется тем, что сама конвекция стремится выравнивать температуру слоев. Средняя скорость поднимающихся и опускающихся газовых масс также незначительна — всего лишь порядка нескольких десятков метров в секунду. Полезно сравнить эту скорость с тепловыми скоростями ионизованных атомов водорода в недрах звезд, которые порядка нескольких сотен километров в секунду. Так как скорость движения газов, участвующих в конвекции, в десятки тысяч раз меньше тепловых скоростей частиц звездного вещества, то давление, вызываемое конвективными потоками, почти в миллиард раз меньше обычного газового давления. Это означает, что конвекция совершенно не влияет на гидростатическое равновесие вещества звездных недр, определяемое равенством сил газового давления и гравитации. Не следует представлять себе конвекцию как некий упорядоченный процесс, где области подъема газа регулярно чередуются с областями его опускания. Характер конвективного движения не «ламинарный», а «турбулентный»; т. е. носит крайне хаотический, беспорядочно меняющийся во времени и пространстве характер. Хаотический характер движения газовых масс приводит к полному перемешиванию вещества. Это означает, что химический состав области звезды, охваченной конвективными движениями, должен быть однородным. Последнее обстоятельство имеет весьма большое значение для многих проблем звездной эволюции. Например, если в результате ядерных реакций в самой горячей (центральной) части конвективной зоны химический состав изменился (например, стало меньше водорода, часть которого превратилась в гелий), то за короткое время это изменение распространится на всю конвективную зону. Таким образом, в «зону ядерных реакций» — центральную область звезды — непрерывно может поступать «свежее» ядерное горячее, что имеет конечно, решающее значение для эволюции звезды[ 22 ]. В то же время вполне могут быть и такие ситуации, когда в центральных, самых горячих областях звезды конвекции нет, что приводит в процессе эволюции к радикальному изменению химического состава этих областей. Об этом более подробно будет идти речь в § 12. Глава 8 Ядерные источники энергии излучения звезд В § 3 мы уже говорили о том, что источниками энергии Солнца и звезд, обеспечивающими их светимость в течение гигантских «космогонических» промежутков времени, исчисляемых для звезд не слишком большой массы миллиардами лет, являются термоядерные реакции. Сейчас мы остановимся на этом важном вопросе более подробно. Основы теории внутреннего строения звезд были заложены Эддингтоном еще тогда, когда источники их энергии были не известны. Мы уже знаем, что ряд важных результатов, касающихся условия равновесия звезд, температуры и давления в их недрах и зависимости светимости от массы, химического состава (определяющего средний молекулярный вес) и непрозрачности вещества, мог быть получен и без знания природы источников звездной энергии. Тем не менее понимание сущности источников энергии совершенно необходимо для объяснения длительности существования звезд в почти неизменном состоянии. Еще более важно значение природы источников звездной энергии для проблемы эволюции звезд, т. е. закономерного изменения их основных характеристик (светимости, радиуса) с течением времени. Только после того как стала ясной природа источников звездной энергии, оказалось возможным понять диаграмму Герцшпрунга — Рессела,— основную закономерность звездной астрономии. Вопрос об источниках звездной энергии был поставлен почти сразу же после открытия закона сохранения энергии, когда стало ясно, что излучение звезд обусловлено какими-то энергетическими превращениями и не может происходить вечно. Неслучайно первая гипотеза об источниках звездной энергии принадлежит Майеру — человеку, открывшему закон сохранения энергии. Он полагал, что источником излучения Солнца является непрерывное выпадение на его поверхность метеорных тел. Расчеты, однако, показали, что этого источника явно недостаточно для обеспечения наблюдаемой светимости Солнца. Гельмгольц и Кельвин пытались объяснить длительное излучение Солнца его медленным сжатием, сопровождающимся освобождением гравитационной энергии. Эта очень важная даже (и особенно!) для современной астрономии гипотеза оказалась, однако, несостоятельной для объяснения излучения Солнца в течение миллиардов лет. Заметим еще, что во времена Гельмгольца и Кельвина никаких разумных идей о возрасте Солнца еще не было. Лишь недавно стало ясно, что возраст Солнца и всей планетной системы около 5 миллиардов лет. На рубеже XIX и XX вв. было сделано одно из величайших открытий в истории человечества — обнаружена радиоактивность. Тем самым открылся совершенно новый мир атомных ядер. Потребовалось, однако, не одно десятилетие, чтобы физика атомного ядра стала на прочную научную основу. Уже к 20-м годам нашего века стало ясно, что источник энергии Солнца и звезд следует искать в ядерных превращениях. Сам Эддингтон тоже так считал, однако указать конкретные ядерные процессы, происходящие в реальных звездных недрах и сопровождаемые выделением нужного количества энергии, тогда еще не было возможности. Насколько несовершенны были тогда знания природы источников звездной энергии, видно хотя бы из того, что Джинс — крупнейший английский физик и астроном начала нашего века,— полагал, что таким источником может быть... радиоактивность. Это, конечно, тоже ядерный процесс, но он, как легко показать, совершенно непригоден для объяснения излучения Солнца и звезд. Это видно хотя бы из того, что такой источник энергии совершенно не зависит от внешних условий — ведь радиоактивность, как хорошо известно, есть процесс спонтанный. По этой причине такой источник никак не мог бы «подстраиваться» под меняющуюся структуру звезды. Другими словами, отсутствовала бы «регулировка» излучения звезды. Вся картина звездного излучения резко противоречила бы наблюдениям. Первым, кто это понял, был замечательный эстонский астроном Э. Эпик, который незадолго до второй мировой войны пришел к выводу, что источником энергии Солнца и звезд могут быть только термоядерные реакции синтеза. Только в 1939 г. известный американский физик Бете дал количественную теорию ядерных источников звездной энергии. Что же это за реакции? В § 7 мы уже упоминали, что в недрах звезд должны происходить термоядерные реакции. Остановимся на этом немного подробнее. Как известно, ядерные реакции, сопровождающиеся превращениями ядер и выделением энергии, происходят при столкновении частиц. Такими частицами могут быть прежде всего сами ядра. Кроме того, ядерные реакции могут происходить и при столкновениях ядер с нейтронами. Однако свободные (т. е. не связанные в ядрах) нейтроны являются неустойчивыми частицами. Поэтому их количество в недрах звезд должно быть ничтожно мало[ 23 ]. С другой стороны, так как водород является самым обильным элементом в звездных недрах и он полностью ионизован, особенно часто будут происходить столкновения ядер с протонами. Для того чтобы протон мог при таком столкновении проникнуть в ядро, с которым он сталкивается, ему надо приблизиться к последнему на расстояние около 10-13 см. Именно на таком расстоянии действуют специфические силы притяжения, «цементирующие» ядро и присоединяющие к нему «чужой», сталкивающийся протон. Но для того, чтобы приблизиться к ядру на столь малое расстояние, протону необходимо преодолеть весьма значительную силу электростатического отталкивания («кулоновский барьер»). Ведь ядро тоже заряжено положительно! Легко подсчитать, что для преодоления этой электростатической силы протону нужно иметь кинетическую энергию, превышающую потенциальную энергию электростатического взаимодействия
Между тем, как мы убедились в § 7, средняя кинетическая энергия тепловых протонов в солнечных недрах составляет всего лишь около 1 кэВ, т. е. в 1000 раз меньше. Протонов с нужной для ядерных реакций энергией в недрах звезд практически не будет. Казалось бы, при такой ситуации никаких ядерных реакций там происходить не может. Но это не так. Дело в том, что согласно законам квантовой механики протоны, энергия которых даже значительно меньше 1000 кэВ, все же, с некоторой небольшой вероятностью, могут преодолеть кулоновские силы отталкивания и попасть в ядро. Эта вероятность быстро уменьшается с уменьшением энергии протона, но она не равна нулю. В то же время число протонов по мере приближения их энергии к средней тепловой будет стремительно расти. Поэтому должна существовать такая «компромиссная» энергия протонов, при которой малая вероятность их проникновения в ядро «компенсируется» их большим количеством. Оказывается, что в условиях звездных недр эта энергия близка к 20 кэВ. Только приблизительно одна стомиллионная доля протонов имеет такую энергию. И все же этого оказывается как раз достаточно, чтобы ядерные реакции происходили с такой скоростью, что выделяющаяся энергия точно соответствовала бы светимости звезд. Мы остановили свое внимание на реакциях с протонами не только потому, что они — самая обильная составляющая вещества звездных недр. Если сталкиваются более тяжелые ядра, у которых заряды значительно больше элементарного заряда протона, кулоновские силы отталкивания существенно увеличиваются, и ядра при T Мы уже говорили в § 3, что сущность ядерных реакций внутри Солнца и звезд состоит в том, что через ряд промежуточных этапов четыре ядра водорода объединяются в одно ядро гелия ( Опишем сначала протон-протонную реакцию. Эта реакция начинается с таких столкновений между протонами, в результате которых получается ядро тяжелого водорода — дейтерия. Даже в условиях звездных недр это происходит очень редко. Как правило, столкновения между протонами являются упругими: после столкновения частицы просто разлетаются в разные стороны. Для того чтобы в результате столкновения два протона слились в одно ядро дейтерия, необходимо, чтобы при таком столкновении выполнялось два независимых условия. Во-первых, надо, чтобы у одного из сталкивающихся протонов кинетическая энергия раз в двадцать превосходила бы среднюю энергию тепловых движений при температуре звездных недр. Как уже говорилось выше, только одна стомиллионная часть протонов имеет такую относительно высокую энергию, необходимую для преодоления «кулоновского барьера». Во-вторых, необходимо, чтобы за время столкновения один из двух протонов успел бы превратиться в нейтрон, испустив позитрон и нейтрино. Ибо только протон с нейтроном могут образовать ядро дейтерия! Заметим, что длительность столкновения всего лишь около 10-21 секунды (оно порядка классического радиуса протона, поделенного на его скорость). Если все это учесть, то получается, что каждый протон имеет реальные шансы превратиться таким способом в дейтерий только раз в несколько десятков миллиардов лет. Но так как протонов в недрах звезд достаточно много, такие реакции, и притом в нужном количестве, будут иметь место. По-другому складывается судьба вновь образовавшихся ядер дейтерия. Они «жадно», всего лишь через несколько секунд, «заглатывают» какой-нибудь близкий протон, превращаясь в изотоп гелия 3Не. После этого возможны три пути (ветви) ядерных реакций. Чаще всего изотоп гелия будет взаимодействовать с подобным себе ядром, в результате чего образуется ядро «обыкновенного» гелия и два протона. Так как концентрация изотопа 3Не чрезвычайно мала, это произойдет через несколько миллионов лет. Напишем теперь последовательность этих реакций и выделяющуюся при них энергию.
Здесь буква Не вся освободившаяся в результате этой цепи реакций энергия передается звезде, так как часть энергии уносится нейтрино. С учетом этого обстоятельства энергия, выделяемая при образовании одного ядра гелия, равна 26,2 МэВ или 4,2 Вторая ветвь протон-протонной реакции начинается с соединения ядра 3Не с ядром «обыкновенного» гелия 4Не, после чего образуется ядро бериллия 7Ве. Ядро бериллия в свою очередь может захватить протон, после чего образуется ядро бора 8В, или захватить электрон и превратиться в ядро лития. В первом случае образовавшийся радиоактивный изотоп 8В претерпевает бета-распад: 8B Еще раз отметим, что подавляющее большинство реакций идет по первой цепи, но роль «побочных» цепей отнюдь не мала, что следует хотя бы из знаменитого нейтринного эксперимента, который будет описан в следующем параграфе. Перейдем теперь к рассмотрению углеродно-азотного цикла. Этот цикл состоит из шести реакций.
Поясним содержание этой таблицы. Протон, сталкиваясь с ядром углерода, превращается в радиоактивный изотоп азота 13N. При этой реакции излучается Во втором столбце приводится энергия, выделяющаяся на каждом этапе углеродно-азотной реакции. Часть этой энергии выделяется в форме нейтрино, возникающих при распаде радиоактивных изотопов 13N и 15O. Нейтрино свободно выходят из звездных недр наружу, следовательно, их энергия не идет на нагрев вещества звезды. Например, при распаде 15O энергия образующегося нейтрино составляет в среднем около 1 МэВ. Окончательно при образовании одного ядра гелия путем углеродно-азотной реакции выделяется (без учета нейтрино) 25 МэВ энергии, а нейтрино уносят около 5% этой величины. В третьем столбце таблицы II приведены значения скорости различных звеньев углеродно-азотной реакции. Для Как уже неоднократно подчеркивалось выше, скорость термоядерных реакций чувствительным образом зависит от температуры. Это и понятно — даже небольшие изменения температуры очень резко сказываются на концентрации необходимых для реакции сравнительно энергичных протонов, энергия которых раз в 20 превышает среднюю тепловую энергию. Для протон-протонной реакции приближенная формула для скорости энерговыделения, рассчитанного на грамм вещества, имеет вид
Эта формула справедлива для сравнительно узкого, но важного интервала температур 11—16 миллионов кельвинов. Для более низких температур (от 6 до 10 миллионов кельвинов) справедлива другая формула:
Основным источником энергии Солнца, температура центральных областей которого близка к 14 миллионам кельвинов, является протон-протонная реакция. Для более массивных, а следовательно, и более горячих звезд существенна углеродно-азотная реакция, зависимость которой от температуры значительно более сильная. Например, для интервала температур 24—36 миллионов кельвинов
Понятно, почему эта формула содержит множителем величину Z — относительную концентрацию тяжелых элементов: углерода и азота. Ведь ядра этих элементов являются катализаторами углеродно-азотной реакции. Обычно суммарная концентрация этих элементов приблизительно в семь раз меньше концентрации всех тяжелых элементов. Последнее обстоятельство учитывается в численном коэффициенте формулы (8.3). Непрерывно идущие в центральных областях звезд ядерные реакции «медленно, но верно» меняют химический состав звездных недр. Главная тенденция этой химической эволюции — превращение водорода в гелий. Помимо этого в процессе углеродно-азотного цикла меняется относительная концентрация различных изотопов углерода и азота до тех пор, пока не установится некоторое определенное равновесие. При таком равновесии количество реакций за единицу времени, приводящих к образованию какого-нибудь изотопа, равно количеству реакций, которые его «разрушают». Однако время установления такого равновесия может быть очень большим. А пока равновесие не установится, относительные концентрации различных изотопов могут меняться в самых широких пределах. Приводим значения равновесных концентраций изотопов, полученные при температуре 13 миллионов кельвинов[ 24 ]:
Вычисленные равновесные концентрации изотопов не зависят от плотности вещества, ибо скорости всех реакций пропорциональны плотности. Первые два изотопных отношения не зависят также и от температуры. Ошибки в вычисленных равновесных концентрациях достигают нескольких десятков процентов, что объясняется неуверенностью в знании вероятности соответствующих реакции. В земной коре отношение Для протон-протонной реакции равновесное состояние наступает по истечении огромного срока в 14 миллиардов лет. Вычисления, выполненные для T = 13 миллионам кельвинов, дают значения
Заметим, что для более низкой температуры T = 8 Кроме протон-протонной и углеродно-азотной реакции, при некоторых условиях могут иметь существенное значение и другие ядерные реакции. Представляют, например, интерес реакции протонов с ядрами легких элементов — дейтерия, лития, бериллия и бора: 6Li + 1H Если температура звездных недр по каким-либо причинам становится очень большой (порядка сотен миллионов кельвинов), что может случиться после того, как практически весь водород «выгорит», источником ядерной энергии становится совершенно новая реакция. Эта реакция получила название «тройной альфа-процесс». При столь высоких температурах сравнительно быстро идут реакции между альфа-частицами, так как «кулоновский барьер» уже легче преодолеть. В этом случае «высота» кулоновского барьера соответствует энергии в несколько миллионов электронвольт. При столкновениях эффективно просачиваться через барьер будут альфа-частицы с энергией порядка ста тысяч электронвольт. Заметим, что энергия тепловых движений частиц при такой температуре порядка десяти тысяч электронвольт. При таких условиях сталкивающиеся альфа-частицы могут образовывать радиоактивный изотоп бериллия 8Be. Этот изотоп очень быстро опять распадается на две альфа-частицы. Но может так случиться, что не успевшее еще распасться ядро 8Be столкнется с третьей альфа-частицей, конечно, при условии, что у последней достаточно высокая энергия, чтобы «просочиться» через кулоновский барьер. Тогда будет иметь место реакция 4He + 8Be Хотя равновесная концентрация изотопа 8Ве совершенно ничтожна (например, при температуре сто миллионов кельвинов на десять миллиардов
где, как и раньше, Y означает парциальную концентрацию гелия в недрах звезды. В случае, когда почти весь водород «выгорел», величина Y довольно близка к единице. Заметим еще, что энергетически «горение» водорода является более выгодным процессом, так как в этом случае на грамм «горючего» выделяется в 10 раз больше энергии.
На рис. 8.1 в логарифмическом масштабе приведена зависимость энерговыделения от температуры для трех важнейших реакций, которые могут проходить в недрах звезд: протон-протонной, углеродно-азотной и «тройного» столкновения альфа-частиц, которое только что обсуждалось. Стрелками указано положение различных звезд, для которых соответствующая ядерная реакция имеет наибольшее значение. Резюмируя этот параграф, мы должны сказать, что успехи ядерной физики привели к полному объяснению природы источников звездной энергии. Принято думать, что богатейший мир атомных ядер стал известен человечеству после выдающегося открытия Беккерелем радиоактивности. С этим фактором, конечно, трудно спорить. Но на протяжении всей своей истории человечество купалось в лучах Солнца. Давно уже стало банальным утверждение, что источником жизни на Земле является Солнце. Но ведь солнечные лучи — это переработанная ядерная энергия. Это означает, что не будь в природе ядерной энергии, не было бы жизни на Земле. Будучи всем обязаны атомному ядру, люди на протяжении долгих тысячелетий даже не подозревали о его существовании. Но, с другой стороны, смотреть — это еще не значит открыть. И мы не покушаемся на славу замечательного французского ученого... Ядерные процессы играют, как мы видели в этом параграфе, фундаментальную роль в длительной, спокойной эволюции звезд, находящихся на главной последовательности. Но, кроме того, их роль является определяющей при быстро протекающих нестационарных процессах взрывного характера, являющихся поворотными этапами в эволюции звезд. Об этом будет идти речь в третьей части этой книги. Наконец, даже, казалось бы, для такой в высшей степени тривиальной и очень «спокойной» звезды, какой является наше Солнце, ядерные реакции открывают возможность объяснения явлений, которые представляются очень далекими от ядерной физики. Об этом речь пойдет в следующем параграфе. Глава 9 Проблемы нейтринного излучения Солнца До сравнительно недавнего времени одна из важнейших проблем астрономии — проблема внутреннего строения и эволюции звезд решалась совместными усилиями астрофизиков-теоретиков и астрономов-наблюдателей. Как уже неоднократно подчеркивалось, эта проблема никоим образом не могла быть решена без непрерывного контроля выводов теории астрономическими наблюдениями. Особенно большое значение для теории имел анализ прецизионных наблюдений блеска и цвета звезд, входящих в состав скоплений (см. § 12). Считалось и считается, что справедливость теории внутреннего строения и эволюции звезд объясняется возможностью на основе этой теории объяснить ряд тонких особенностей диаграммы Герцшпрунга — Рессела для различных скоплений звезд, имеющих различный возраст. Все же неопределенное ощущение неудовлетворительности, несомненно, остается. В идеале было бы неплохо иметь возможность непосредственно получить основные характеристики звездных недр путем прямых наблюдений. Еще сравнительно недавно сама возможность «заглянуть» в недра звезд представлялась по меньшей мере совершенно фантастической. Огромная толща вещества звезды делает ее непрозрачной для всех видов электромагнитного излучения, включая самые жесткие гамма-лучи. Миллионы лет требуется квантам, генерируемым в центральных областях звезд (благодаря происходящим там ядерным реакциям), чтобы «просочиться» к поверхностным слоям и выйти наружу в межзвездное пространство. За это время кванты, взаимодействуя с веществом звезды, испытывают огромное количество поглощений и переизлучений, претерпевая при этом серьезные трансформации. Если первоначально их частоты соответствовали рентгеновскому диапазону, то, выходя из поверхности звезды, они становятся гораздо «мягче» и частоты их лежат уже в оптическом и непосредственно примыкающих к нему инфракрасном и ультрафиолетовом диапазонах. Другими словами, их свойства уже совсем не отражают свойств среды, в которой они первоначально возникли. Казалось бы, нет никакой возможности получить какую-либо информацию непосредственно из недр звезды. Однако столь богатое «чудесами» развитие физики в нашем столетии совершенно неожиданно открыло возможность хотя бы в принципе подойти к решению этой, считавшейся неразрешимой проблемы. В 1931 г. швейцарский физик-теоретик Вольфганг Паули, исходя из твердого убеждения в выполнении законов сохранения для элементарных процессов и анализируя тогда во многом еще не ясное явление После этого открытия физика нейтрино значительно продвинулась вперед. Как и всякая «порядочная» элементарная частица, нейтрино обладает «двойником» — античастицей, получившей название «антинейтрино». Выдающийся советский физик академик Б. М. Понтекорво теоретически предсказал существование двух «сортов» нейтрино — «электронных» и «мюонных». Очень скоро это предсказание блестяще оправдалось на опыте. Б. М. Понтекорво был также первым, кто указал на важность нейтрино для изучения звездных и в первую очередь солнечных недр. Теория термоядерных реакций, происходящих в центральных областях Солнца, основы которой были изложены в § 8, позволяет довольно надежно оценить величину потока солнечных нейтрино на Земле. В самом деле, как уже неоднократно подчеркивалось выше, суть термоядерных реакций, происходящих в недрах нашего светила, сводится к тому, что четыре протона объединяются в одну альфа-частицу. При этом испускаются два нейтрино. При каждом таком «объединении» выделяется около 25 МэВ энергии, которая в конечном результате выделяется в межзвездное пространство, обеспечивая светимость Солнца. Поэтому полное количество нейтрино, образующихся в недрах Солнца, N = 2L Однако ничтожно малая вероятность взаимодействия солнечных нейтрино с веществом делает эксперименты по их обнаружению исключительно трудными. Идея такого эксперимента была предложена еще в 1946 г. Б. М. Понтекорво. Обнаружение нейтрино может быть основано на реакции
где 37Cl — устойчивый изотоп хлора, а 37Ar — радиоактивный изотоп аргона. Эта реакция называется «обратный бета-распад». Хотя вероятность поглощения нейтрино изотопом хлора весьма мала, все же на практике она оказывается пока единственно возможной для обнаружения солнечных нейтрино. В качестве «рабочего вещества», достаточно богатого изотопом «хлор-37», начиная с 1955 г. используется прозрачная жидкость перхлорэтилен (или «четыреххлористый углерод»), химическая формула которой C2Cl4. Эта довольно дешевая жидкость широко используется в «бытовой» химии как средство очистки поверхностей. Первые опыты по обнаружению нейтрино этим методом были «нацелены» отнюдь не на Солнце, а на ядерные реакторы, излучающие огромное количество нейтрино. Задачей этих опытов, поставленных выдающимся американским физиком-экспериментатором Дэвисом, было «научиться» различать нейтрино и антинейтрино. Последние изотопом 37Cl не поглощаются. В качестве детектора Дэвис использовал сравнительно небольшую емкость в 3900 литров перхлорэтилена. Сущность эксперимента состояла в оценке количества ядер радиоактивного изотопа 37Ar, которые образуются в емкости, наполненной перхлорэтиленом. Такая оценка производится методами современной радиохимии. Хотя основная цель эксперимента и не имела отношения к астрономии, тем не менее, как «побочный продукт», Дэвис впервые получил оценку верхней границы потока солнечных нейтрино, которая, конечно, была еще слишком груба. Чувствительность первого эксперимента Дэвиса была примерно в тысячу раз ниже ожидаемого потока солнечных нейтрино в том диапазоне энергии, который поглощается изотопом 37Cl.
Последняя оговорка весьма существенна. Выше мы оценили величину ожидаемого полного потока солнечных нейтрино. Однако перхлорэтиленовый детектор способен поглощать далеко не все солнечные нейтрино с одинаковой эффективностью. Между тем энергетический спектр солнечных нейтрино весьма чувствительным образом зависит от физических условий в недрах Солнца, т. е. от температуры, плотности и химического состава. Другими словами, энергетический спектр солнечных нейтрино, а следовательно, скорость образования в перхлорэтилене радиоактивных ядер 37Ar сильно зависит от модели солнечных недр. Начиная с 1955 г. Дэвис. и его сотрудники упорно работали над повышением чувствительности перхлорэтиленового детектора нейтрино. В результате их усилий в этом направлении чувствительность детектора увеличилась к настоящему времени почти в 30 000 раз! В его современном виде нейтринный детектор представляет собой грандиозное сооружение (рис. 9.1). Гигантский резервуар, наполненный жидким перхлорэтиленом, имеет объем около 400 кубометров, что близко к объему нормального 25-метрового плавательного бассейна. Установка расположена на дне глубокой старой шахты, пробитой в скальном грунте. Глубина шахты превышает 1,5 км, что соответствует экранировке установки эквивалентным слоем воды толщиной около 4,5 км. Расположение детектора глубоко под землей диктуется необходимостью свести к минимуму помехи, приводящие к образованию радиоактивных изотопов аргона без поглощения ядрами хлора нейтрино. Указанные помехи вызываются проникающей компонентой космических лучей. Мю-мезоны, входящие в состав этой компоненты, взаимодействуя с веществом, порождают быстрые протоны, которые, сталкиваясь с ядрами хлора, образуют радиоактивный изотоп 37Ar. Современная чувствительность нейтринного детектора определяется прежде всего величиной «космического» фона, приводящего к образованию описанным выше способом «паразитных» ядер 37Ar. Некоторое понятие о чувствительности этой гигантской установки может дать тот факт, что из-за облучения солнечными нейтрино во всем огромном бассейне перхлорэтилена одновременно присутствуют всего лишь несколько десятков ядер радиоактивного изотопа 37Ar. Заметим в этой связи, что период полураспада этого изотопа около 35 дней. Это ничтожное количество 37Ar удается выделить из «бассейна» путем «продувания» его гелием, после чего изотопы аргона выделяются из гелия химическим путем. Вся эта процедура, конечно, сопряжена с серьезными экспериментальными трудностями, которые Дэвис и его коллеги успешно преодолели. Едва ли не самым парадоксальным следствием опытов Дэвиса и его коллег является неожиданно малое значение потока солнечных нейтрино. По состоянию вопроса на 1982 г. можно было утверждать, что количество поглощенных солнечных нейтрино за одну секунду, рассчитанное на один поглощающий атом хлора, равно (2,2 ± 0,4) Это расхождение между ожидаемым результатом и данными наблюдений представляется довольно большим. Конечно, часть этого расхождения следует искать в несовершенстве теорий, как чисто физических, так и астрономических. Чисто физической является задача вычисления вероятности поглощения хлором солнечных нейтрино. Эта вычисленная вероятность, однако, подкрепляется результатами прямых лабораторных экспериментов, так что нет оснований сомневаться в ее правильности. Возможные ошибки здесь вряд ли превышают 10%. Более серьезным является вопрос о точности ныне принятой модели внутренних областей Солнца. Как мы уже упоминали выше, от этой модели зависит энергетический спектр солнечных нейтрино, а следовательно, и количество образовавшихся в бассейне перхлорэтилена изотопов радиоактивного аргона. Например, скорость образования нейтрино при бета-распаде 8B (образующихся при одной из ветвей протон-протонной реакции; см. § 8) зависит от температуры T приблизительно как T13, т. е. очень сильно. Между тем перхлорэтиленовый детектор регистрирует преимущественно нейтрино, образовавшиеся при распаде 8B, так как они обладают наибольшей энергией ( В принципе при современном уровне теории модель любой звезды, находящейся на главной последовательности, может быть построена достаточно точно, если известна масса звезды- и распределение ее химического состава по всей толще. Для Солнца масса известна с высокой точностью, в то время как имеется достаточно большая неопределенность в распределении его химического состава. Последнее зависит от характера перемешивания вещества в недрах Солнца. Скорее всего, относительное обилие гелия в ядре Солнца выше, чем в более наружных слоях. Разница в обилиях гелия в центральных областях и на периферии зависит также от возраста Солнца, который принимается равным 4,7 миллиарда лет. Для построения моделей имеют также большое значение полученные из лабораторных данных скорости тех или иных ядерных реакций, происходящих в солнечных недрах. Например, переоценка времени жизни свободных нейтронов, которая произошла в 1967 г., и уточнение лабораторных данных о скорости некоторых важных для астрофизики ядерных реакций заставили несколько пересмотреть значение скорости протон-протонной реакции — важнейшей термоядерной реакции в недрах Солнца. Предложенные в последние годы модели Солнца дают весьма разные значения ожидаемого в экспериментах Дэвиса количества поглощенных нейтрино — от 30 до 6 s. n. u. Однако даже последнее, наинизшее значение все же в несколько раз превосходит наблюдаемую верхнюю границу. Означает ли столь неожиданный результат экспериментов по обнаружению солнечных нейтрино, что наши представления о внутренней структуре и эволюции звезд неверны и нуждаются в коренном пересмотре? Пока для такого вывода оснований нет. Но есть проблема объяснения результатов опытов Дэвиса. Прежде всего не все возможности построения модели Солнца исчерпаны. В принципе малое значение нейтринного потока, фиксируемое перхлорэтиленовым детектором (реагирующим, как мы уже говорили выше, главным образом на нейтрино, образующиеся при радиоактивном бета-распаде 8B в «боковой» ветви протон-протонной реакции), можно объяснить предположением, что относительное обилие тяжелых элементов в недрах Солнца по крайней мере в 20 раз меньше наблюдаемого значения на его поверхности. При малом обилии тяжелых элементов вещество солнечных недр становится более прозрачным, температура уменьшается, а следовательно, уменьшается поток нейтрино, возникающих при распаде 8B. Сразу же, однако, возникает трудность: вычисленное на основе этого предположения первоначальное обилие гелия в веществе, из которого образовалось Солнце, должно быть в несколько раз меньше наблюдаемого обилия гелия в межзвездной среде. Нелегко также представить себе, каким способом образовался столь большой «дефицит» тяжелых элементов в недрах Солнца по сравнению с его поверхностью. Все же можно не сомневаться, что попытки объяснить результаты экспериментов Дэвиса разного рода модификациями солнечной модели будут продолжаться и, кто знает, возможно, приведут к успеху. Другая возможность объяснения отрицательного результата опытов по обнаружению солнечных нейтрино состоит в ревизии основных представлений о природе нейтрино. Так, например, была высказана гипотеза, что нейтрино — нестабильная частица. Эта гипотеза требует признания у нейтрино хотя и малой, но конечной массы покоя. Если предположить, что период полураспада нейтрино меньше нескольких сотен секунд, то ясно, что образовавшиеся в недрах Солнца нейтрино просто не дойдут до Земли. Разновидностью этого типа гипотез является «гипотеза осцилляции», предложенная Б. М. Понтекорво. Суть этой гипотезы сводится к тому, что испущенные Солнцем «электронные» нейтрино могут превращаться в «мюонные», на которые детектор Дэвиса не реагирует. Однако такие гипотезы требуют коренного изменения существующих представлений о свойствах элементарных частиц. Уж слишком велика цена, которую надо заплатить за объяснение отрицательного результата опытов Дэвиса. Вряд ли эта гипотеза (так же, как и другие родственные ей) соответствует действительности[ 25 ]. Совершенно другой подход к обсуждаемой здесь проблеме содержится в гипотезе Фаулера, высказанной в конце 1972 г. Он предположил, что несколько миллионов лет назад во внутренних слоях Солнца произошло сравнительно быстрое, как бы «скачкообразное» перемешивание вещества. Таким образом, в течение последних нескольких миллионов лет недра Солнца находятся в необычном, как бы переходном состоянии. Через несколько миллионов лет физические условия в недрах Солнца вернутся к первоначальному состоянию, до того как такое внезапное перемешивание произошло. Отвлекаясь пока от анализа причин, повлекших за собой такое «катастрофическое» перемешивание, рассмотрим, какие это повлечет за собой последствия для проблемы солнечных нейтрино. Вся суть гипотезы Фаулера состоит в том, что поток нейтрино от Солнца определяется «мгновенным» состоянием солнечных недр. Это означает, что если по какой-либо причине изменилась температура солнечных недр, это сразу же отразится на выходящем из Солнца потоке нейтрино. Совсем по-другому будет вести себя поток фотонного излучения от Солнца. Как уже неоднократно подчеркивалось выше, образовавшимся в центральных областях Солнца фотонам требуются миллионы лет, чтобы просочиться наружу и выйти в межзвездное пространство. Таким образом, в принципе, возможна такая ситуация: внезапно температура в центре Солнца падает, сразу же резко упадет поток нейтрино, в то время как светимость Солнца останется неизменной. Идея Фаулера представляется нам в высшей степени плодотворной. Развитие гипотезы Фаулера содержится в работе Эзера и Камерона. Если предположить, что по какой-либо причине резко увеличилось энерговыделение в центре Солнца, обусловленное ядерными реакциями, то это повлечет за собой быстрое расширение солнечного ядра, температура которого понизится. Понижение температуры недр Солнца повлечет за собой уменьшение скорости всех термоядерных реакций. После того как избыточная энергия покинет пределы центральных областей Солнца, последние вернутся к своему первоначальному состоянию и поток солнечных нейтрино восстановится. Каким же образом может произойти резкое увеличение энерговыделения в центральной области Солнца? Оказывается, здесь большое значение может иметь такая ничтожно малая примесь к веществу солнечных недр, как редкий изотоп гелия 3He. В обычных условиях в недрах Солнца концентрация этого изотопа поддерживается динамическим равновесием между ядерными реакциями, ведущими к его образованию и уничтожению. Между тем, как уже обсуждалось в § 8, концентрация 3He имеет большое значение для идущей в недрах Солнца протон-протонной реакции, обеспечивающей почти всю светимость Солнца. Оказывается, что чем выше температура, тем ниже равновесная концентрация 3He. Отсюда непосредственно следует, что равновесная концентрация 3He должна расти по мере удаления от центра Солнца, однако, начиная с некоторого расстояния от центра, рост концентрации 3He прекращается: температура оказывается уже слишком низкой для того, чтобы равновесная концентрация успела установиться за те Причиной внезапного перемешивания солнечных недр может быть постепенное накопление некоторой «неустойчивости», которая, дойдя до определенного предела, как бы «сбрасывается». Например, эта причина может быть связана с циркуляцией вещества солнечных недр в меридианном направлении, которая будет как бы «транспортировать» вращательный момент Солнца от его периферических слоев к центру. В результате центральные области Солнца начнут вращаться значительно быстрее, чем периферия. Такая ситуация должна приводить к неустойчивости, которая будет «сбрасываться» перемешиванием. Гипотеза рассматривалась японским теоретиком Сакураи. Важной особенностью этого механизма внезапного перемешивания является его периодичность. Ведь после того как накопившаяся неустойчивость будет «сброшена», она опять начнет накапливаться, так как «меридианная» циркуляция в солнечных недрах будет продолжаться! По оценкам Эзера и Камерона время между такими сравнительно быстрыми процессами перемешивания солнечных недр порядка сотни миллионов лет. Это означает, что за время эволюции нашего светила такие процессы происходили несколько десятков раз. Так как длительность фазы, когда по причине внезапного перемешивания температура солнечных недр становится ниже «нормальной», порядка десяти миллионов лет, то примерно 10% всего времени своей эволюции солнечные недра должны находиться в таком «минимальном» состоянии. Выходит, что нам особенно «повезло», раз мы живем в такую эпоху эволюции Солнца. Это замечание, как мы увидим ниже, может иметь гораздо более глубокий смысл, чем это кажется на первый взгляд...
Американские авторы выполнили численные расчеты вариаций нейтринного излучения Солнца со временем в процессе такого перемешивания. Результаты вычислений приведены на рис. 9.2. Как мы видим из этого графика, перед перемешиванием «нормальное» Солнце излучает поток нейтрино, который соответствовал бы примерно 10 единицам s. n. u. на перхлорэтиленовом детекторе Дэвиса. В середине фазы перемешивания поток падает до значения, которое немного, но все-таки ниже наблюдаемого предела. Однако Эзер и Камерон не ограничиваются только конкретизацией идеи Фаулера. Они идут значительно дальше. Дело в том, что расширение центральной области Солнца должно неизбежно отразиться на его светимости, т. е. на потоке его фотонного излучения. Кроме того, должен немного уменьшиться его радиус. Хотя температура поверхности Солнца почти не изменится, его светимость будет заметно уменьшаться во время фазы перемешивания. Результаты соответствующих вычислений приведены на рис. 9.3. Как видим, изменения светимости должны быть весьма значительными. Возникает совершенно естественный вопрос: а не отразились ли эти циклические «провалы» солнечной светимости на геологической истории Земли?
Если предлагаемое Фаулером объяснение отрицательного результата опытов по обнаружению солнечных нейтрино правильно, нынешний уровень солнечного излучения следует считать значительно более низким, чем «нормальный» уровень. Следующее из рис. 9.3 уменьшение уровня солнечной светимости против «нормального» должно соответствовать уменьшению равновесной температуры Земли в отношении (L1/L Но ведь это соответствует действительности! По геологическим данным ледниковый период на нашей планете длится вот уже два миллиона лет. Сейчас на Земле относительно тепло, потому что мы живем в сравнительно короткое (длительность около 15 000 лет) межледниковое время[ 26 ]. Только сравнительно недавно геологи доказали, что оледенения Земли всегда носили глобальный характер, т. е. происходили одновременно на обеих ее полушариях. Это означает, что причиной ледниковых периодов может быть только некоторый космический фактор. Если сейчас начинают понимать, что даже земная метеорология управляется солнечной активностью, можно ли сомневаться в том, что великие оледенения Земли были обусловлены гораздо более значительными изменениями уровня солнечного излучения? Мы говорим «оледенения» во множественном числе. Ведь уже давно известно, что в далеком геологическом прошлом Земли (например, в архейское время) также были великие оледенения. Доказано, что такие оледенения на нашей планете происходили периодически каждые 200—300 миллионов лет, причем длительность ледниковых периодов была около 10 миллионов лет. Как видим, именно к такой картине приводит развитие идеи Фаулера, выполненное Эзером и Камероном! Приходится только удивляться неожиданным характерам взаимосвязи явлений в природе. Удивительным и совершенно неожиданным образом проблемы нейтринной астрономии могут быть связаны с фундаментальнейшей проблемой геологии, до последнего времени, несмотря на многочисленные попытки, остававшейся нерешенной. Стоит еще подумать о том, что ледниковый период был «колыбелью» человечества. Вряд ли бы австралопитеки стали в итоге длительного процесса эволюции людьми, если бы не было ледникового периода. Даже если дальнейшее развитие науки приведет к другому объяснению отрицательных результатов опытов Дэвиса, объяснение ледниковых периодов, которое мы сейчас обсуждали, может остаться верным и поражать нас своим изяществом. Глава 10 Как устроены белые карлики? В § 1, когда мы обсуждали физические свойства различных звезд, нанесенных на диаграмму Герцшпрунга — Рессела, было уже обращено внимание на так называемые «белые карлики». Типичным представителем этого класса звезд является знаменитый спутник Сириуса, так называемый «Сириус В». Тогда же подчеркивалось, что эти странные звезды — отнюдь не редкая категория каких-то патологических «уродцев» в нашей Галактике. Наоборот, это весьма многочисленная группа звезд. Их в Галактике должно быть по крайней мере несколько миллиардов, а может быть, и все десять миллиардов, т. е. до 10% всех звезд нашей гигантской звездной системы. Следовательно, белые карлики должны были образоваться в результате какого-то закономерного процесса, который имел место у заметной части звезд. А отсюда следует, что наше понимание мира звезд будет весьма далеким от полноты, если мы не поймем природу белых карликов и не выясним вопроса об их происхождении. Впрочем, в этом параграфе мы не будем обсуждать вопросов, связанных с проблемой образования белых карликов,— это будет сделано в § 13. Наша задача пока что — попытаться понять природу этих удивительных объектов. Основные особенности белых карликов таковы: a. Масса не слишком отличается от массы Солнца при радиусе, в сотню раз меньшем, чем у Солнца. Размеры белых карликов одного порядка с размерами земного шара. b. Отсюда следует огромная средняя плотность вещества, доходящая до 106—107 г/см3 (т. е. до десятка тонн, «запрессованных» в кубическом сантиметре!). c. Светимость белых карликов очень мала: в сотни и тысячи раз меньше солнечной. При первой же попытке проанализировать условия в недрах белых карликов мы сразу же сталкиваемся с очень большой трудностью. В § 6 была установлена связь между массой звезды, ее радиусом и центральной температурой (см. формулу (6.2)). Так как последняя должна быть обратно пропорциональна радиусу звезды, то центральные температуры белых карликов, казалось бы, должны достигать огромных значений порядка многих сотен миллионов кельвинов. При таких чудовищных температурах там должно было выделяться непомерно большое количество ядерной энергии. Даже если предположить, что весь водород там «выгорел», тройная гелиевая реакция должна быть весьма эффективной. Выделяющаяся при ядерных реакциях энергия обязана «просачиваться» на поверхность и уходить в межзвездное пространство в форме излучения, которое должно было быть исключительно мощным. А между тем светимость белых карликов совершенно ничтожна, на несколько порядков меньше, чем у «обычных» звезд той же массы. В чем тут дело? Попытаемся разобраться в этом парадоксе. Прежде всего столь сильное расхождение между ожидаемой и наблюдаемой светимостью означает, что формула (6.2) § 6 попросту неприменима к белым карликам. Вспомним теперь, какие основные допущения были сделаны при выводе этой формулы. Прежде всего предполагалось, что звезда находится в состоянии равновесия под действием двух сил: гравитации и газового давления. Не приходится сомневаться, что белые карлики находятся в состоянии гидростатического равновесия, которое мы подробно обсуждали в § 6. В противном случае за короткое время они перестали бы существовать: рассеялись в межзвездном пространстве, если давление превышало бы гравитацию, либо сжались «в точку», если гравитация не была бы скомпенсирована давлением газа. Не приходится также сомневаться в универсальности закона всемирного тяготения: сила гравитации действует повсеместно и она не зависит ни от каких других свойств вещества, кроме его количества. Тогда остается только одна возможность: усомниться в зависимости газового давления от температуры, которую мы получили с помощью хорошо известного закона Клапейрона. Этот закон справедлив для идеального газа. В § 6 мы убедились, что вещество недр обычных звезд с достаточной точностью можно считать идеальным газом. Следовательно, логический вывод состоит в том, что очень плотное вещество недр белых карликов уже не является идеальным газом. Правда, резонно вообще усомниться, является ли это вещество газом? Может быть, это жидкость или твердое тело? Легко убедиться, что это не так. Ведь в жидкостях и твердых телах плотно упакованы атомы, которые соприкасаются своими электронными оболочками, имеющими не такие уж маленькие размеры: порядка 10-8 см. Ближе чем на такое расстояние атомные ядра, в которых сосредоточена практически вся масса атомов, «придвинуться» друг к другу не могут. Отсюда непосредственно следует, что средняя плотность твердого или жидкого вещества не может значительно превосходить Итак, вещество недр белых карликов — это очень плотный ионизованный газ. Однако из-за огромной плотности его физические свойства резко отличаются от свойств идеального газа. Не следует путать это отличие свойств со свойствами реальных газов, о которых достаточно много говорится в курсе физики. Специфические свойства ионизованного газа при сверхвысоких плотностях определяются вырождением. Это явление находит себе объяснение только в рамках квантовой механики. Классической физике понятие «вырождение» чуждо. Что же это такое? Чтобы ответить на этот вопрос, нам придется сначала немного остановиться на особенностях движения электронов в атоме, описываемых законами квантовой механики. Состояние каждого электрона в атомной системе определяется заданием квантовых чисел. Эти числа суть главное квантовое число n, определяющее энергию электрона в атоме, квантовое число l, дающее значение орбитального вращательного момента электрона, квантовое число m, дающее значение проекции этого момента на физически выделенное направление (например, направление магнитного поля), и, наконец, квантовое число s, дающее значение собственного вращательного момента электрона (спин). Фундаментальным законом квантовой механики является принцип Паули, запрещающий для любой квантовой системы (например, сложного атома) двум каким-либо электронам иметь все квантовые числа одинаковыми. Поясним этот принцип на простой полуклассической боровской модели атома. Совокупность трех квантовых чисел (кроме спина) определяет орбиту электрона в атоме. Принцип Паули, применительно к этой модели атома, запрещает находиться на одной и той же квантовой орбите более чем двум электронам. Если на такой орбите находятся два электрона, то у них должны быть противоположно ориентированные спины. Это означает, что хотя три квантовых числа у таких электронов могут совпадать, квантовые числа, характеризующие спины электронов, должны быть различны. Принцип Паули имеет огромное значение для всей атомной физики. В частности, только на основе этого принципа можно понять все особенности периодической системы элементов Менделеева. Принцип Паули имеет универсальное значение и применим ко всем квантовым системам, состоящим из большого числа тождественных частиц. Примером такой системы, в частности, являются обыкновенные металлы при комнатных температурах. Как известно, в металлах внешние электроны не связаны с «собственными» ядрами, а как бы «обобществлены». Они движутся в сложном электрическом поле ионной решетки металла. В грубом, полуклассическом приближении можно представить, что электроны движутся по некоторым, правда, весьма сложным траекториям, И конечно, для таких траекторий тоже должен выполняться принцип Паули. Это означает, что по каждой из упомянутых выше электронных траекторий может двигаться не больше двух электронов, которые должны отличаться своими спинами. Необходимо подчеркнуть, что согласно квантовомеханическим законам число таких возможных траекторий хотя и очень велико, но конечно. Следовательно, далеко не все геометрически возможные орбиты реализуются. На самом деле, конечно, наше рассуждение является весьма упрощенным. Мы говорили выше о «траекториях» для наглядности. Вместо классической картины движения по траектории квантовая механика говорит только о состоянии электрона, описываемого несколькими совершенно определенными («квантовыми») параметрами. В каждом из возможных состояний электрон имеет некоторую определенную энергию. В рамках нашей модели движения по траекториям принцип Паули можно сформулировать еще так: по одной и той же «дозволенной» траектории могут двигаться с одинаковыми скоростями (т. е. иметь одинаковую энергию) не больше двух электронов. Применительно к сложным, многоэлектронным атомам принцип Паули позволяет понять, почему у них электроны не «ссыпались» на самые «глубокие» орбиты, энергия которых минимальна. Другими словами, он дает ключ к пониманию строения атома. Точно так же обстоит дело и в случае электронов в металле, и в случае вещества недр белых карликов. Если бы одно и то же количество электронов и атомных ядер заполняло достаточно большой объем, то «для всех хватило бы места». Но представим себе теперь, что этот объем ограничен. Тогда только небольшая часть электронов заняла бы все возможные для их движения траектории, число которых по необходимости ограничено. Остальные электроны должны были бы двигаться по тем же самым траекториям, которые уже «заняты». Но в силу принципа Паули они будут двигаться по этим траекториям с большими скоростями и, следовательно, обладать большей энергией. Дело обстоит совершенно так же, как в многоэлектронном атоме, где из-за того же принципа «избыточные» электроны обязаны двигаться по орбитам с большей энергией. В куске металла или в каком-нибудь объеме внутри белого карлика число электронов больше числа дозволенных траекторий движения. Иное дело в обычном газе, в частности, в недрах звезд главной последовательности. Там число электронов всегда меньше числа дозволенных траекторий. Поэтому электроны могут двигаться по разным траекториям с различными скоростями, как бы «не мешая» друг другу. Принцип Паули в этом случае не отражается на их движении. В таком газе устанавливается максвеллово распределение скоростей и выполняются хорошо известные из школьной физики законы газового состояния вещества, в частности, закон Клапейрона. Если «обычный» газ сильно сжать, то число возможных траекторий для электронов станет значительно меньше и, наконец, наступит такое состояние, когда на каждую траекторию придется больше двух электронов. В силу принципа Паули эти электроны обязаны иметь различные скорости, превышающие некоторое критическое значение. Если теперь сильно охладить этот сжатый газ, то скорости электронов отнюдь не уменьшатся. В противном случае, как легко понять, принцип Паули перестал бы выполняться. Даже вблизи абсолютного нуля скорости электронов в таком газе оставались бы большими. Газ, обладающий такими необычайными свойствами, называется вырожденным. Поведение такого газа целиком объясняется тем, что его частицы (в нашем случае — электроны) занимают все возможные траектории и движутся по ним «по необходимости» с весьма большими скоростями. В противоположность вырожденному газу скорости движения частиц в «обычном» газе при уменьшении его температуры становятся очень маленькими. В соответствии с этим уменьшается и его давление. Как же обстоит дело с давлением вырожденного газа? Для этого вспомним, что мы называем давлением газа. Это импульс, который частицы газа передают за одну секунду времени при столкновениях некоторой «стенке», ограничивающей его объем. Отсюда ясно, что давление вырожденного газа должно быть очень велико, так как скорости образующих его частиц велики. Даже при очень низких температурах давление вырожденного газа должно оставаться большим, так как скорости его частиц, в отличие от обычного газа, почти не уменьшаются с уменьшением температуры. Следует ожидать, что давление вырожденного газа мало зависит от его температуры, так как скорость движения образующих его частиц определяется прежде всего принципом Паули. Наряду с электронами в недрах белых карликов должны быть «оголенные» ядра, а также сохранившие «внутренние» электронные оболочки сильно ионизованные атомы. Оказывается, что для них количество «дозволенных» траекторий всегда больше числа частиц. Поэтому они образуют не вырожденный, а «нормальный» газ. Скорости их определяются температурой вещества белых карликов и всегда много меньше, чем скорости электронов, обусловленных принципом Паули. Поэтому в недрах белых карликов давление обусловлено только вырожденным электронным газом. Отсюда следует, что равновесие белых карликов почти не зависит от их температуры. Как показывают квантовомеханические расчеты, давление вырожденного электронного газа, выраженное в атмосферах, определяется формулой
где постоянная K = 3 Условием применимости формулы (10.1) является малость тепловых скоростей электронов по сравнению со скоростями, обусловленными «вырождением». При очень высоких температурах формула (10.1) должна переходить в формулу Клапейрона (6.2). Если давление, полученное для газа с плотностью
или
где
Если, например, температура T = 300 К (комнатная температура), то a. В недрах обычных звезд, где плотность хотя и высока, но заведомо ниже 1000 г/см3, газ не вырожден. Это обосновывает применимость обычных законов газового состояния, которыми мы широко пользовались в § 6. b. У белых карликов средние, а тем более центральные плотности заведомо больше 1000 г/см3. Поэтому обычные законы газового состояния для них неприменимы. Для понимания белых карликов необходимо знать свойства вырожденного газа, описываемые уравнением его состояния (10.1). Из этого уравнения прежде всего следует, что структура белых карликов практически не зависит от их температуры. Так как, с другой стороны, светимость этих объектов определяется, их температурой (например, скорость термоядерных реакций зависит от температуры), то мы можем сделать вывод, что структура белых карликов не зависит и от светимости. В принципе, белый карлик может существовать (т. е. находиться в равновесной конфигурации) и при температуре, близкой к абсолютному нулю. Мы приходим, таким образом, к выводу, что для белых карликов, в отличие от «обычных» звезд, не существует зависимость «масса — светимость». Для этих необычных звезд, однако, существует специфическая зависимость «масса — радиус». Подобно тому как сделанные из одного какого-либо металла шары равной массы должны иметь равные диаметры, размеры белых карликов с одинаковой массой также должны быть одинаковы. Это утверждение, очевидно, несправедливо для других звезд: звезды-гиганты и звезды главной последовательности могут иметь одинаковые массы, но существенно разные диаметры. Такое отличие белых карликов от остальных звезд объясняется тем, что температура почти не играет никакой роли в их гидростатическом равновесии, которое и определяет структуру.
Коль скоро это так, должно быть некоторое универсальное соотношение, связывающее массы белых карликов и их радиусы. В нашу задачу не входит вывод этой важной зависимости, который далеко не является элементарным. Сама зависимость (в логарифмическом масштабе) представлена на рис. 10.1. На этом рисунке кружки и квадратики отмечают положение некоторых белых карликов с известными массами и радиусами. Приведенная на этом рисунке зависимость массы и радиуса для белых карликов имеет две любопытные особенности. Во-первых, из нее следует, что чем больше масса белого карлика, тем меньше его радиус. В этом отношении белые карлики ведут себя иначе, чем шары, выполненные из одного блока металла... Во-вторых, у белых карликов существует предельное допустимое значение массы[ 27 ]. Теория предсказывает, что в природе не могут существовать белые карлики, масса которых превышала бы 1,43 массы Солнца[ 28 ]. Если масса белого карлика приближается к этому критическому значению со стороны меньших масс, то его радиус будет стремиться к нулю. Практически это означает, что начиная с некоторой массы давление вырожденного газа уже не может уравновесить силу гравитации и звезда катастрофически сожмется. Этот результат имеет исключительно большое значение для всей проблемы звездной эволюции. Поэтому стоит остановиться на нем несколько подробнее. По мере увеличения массы белого карлика его центральная плотность будет все более и более расти. Вырождение электронного газа будет становиться все сильнее. Это значит, что на одну «дозволенную» траекторию будет приходиться все большее число частиц. Им будет очень «тесно» и они будут (дабы не нарушать принцип Паули!) двигаться все с большими и большими скоростями. Эти скорости станут довольно близкими к скорости света. Возникнет новое состояние вещества, которое называется «релятивистским вырождением». Уравнение состояния такого газа изменится — оно уже не будет больше описываться формулой (10.1). Вместо (10.1) будет иметь место соотношение
Для оценки создавшейся ситуации положим, как это делалось в § 6,
Между тем сила гравитации равна Допустим теперь, что масса меньше критической. Тогда сила, обусловленная давлением, будет больше гравитационной, следовательно, звезда начнет расширяться. В процессе расширения релятивистское вырождение сменится обычным «нерелятивистским» вырождением. В этом случае из уравнения состояния P Этот качественный анализ иллюстрирует, с одной стороны, необходимость существования зависимости масса — радиус для белых карликов и ее характер (т. е. то, что радиус тем меньше, чем больше масса), а, с другой стороны, обосновывает существование предельной массы, что является следствием с неизбежностью наступающего релятивистского вырождения. До каких пор могут сжиматься звезды с массой, большей, чем 1,2 солнечной массы? Эта увлекательная, ставшая в последние годы весьма актуальной, проблема будет обсуждаться в § 24. Вещество недр белых карликов отличается высокой прозрачностью и теплопроводностью. Хорошая прозрачность этого вещества опять-таки объясняется принципом Паули. Ведь поглощение света в веществе связано с изменением состояния электронов, обусловленном их переходами с одной орбиты на другую. Но если подавляющее большинство «орбит» (или «траекторий») в вырожденном газе «занято», то такие переходы весьма затруднены. Только очень немногие, особенно быстрые электроны в плазме белого карлика могут поглощать кванты излучения. Теплопроводность вырожденного газа велика — тому примером служат обыкновенные металлы. По причине очень высоких прозрачности и теплопроводности в веществе белого карлика не могут возникать большие перепады температуры. Почти весь перепад температуры, если двигаться от поверхности белого карлика к его центру, происходит в очень тонком, наружном слое вещества, который находится в невырожденном состоянии. В этом слое, толщина которого порядка 1% от радиуса, температура возрастает от нескольких тысяч кельвинов на поверхности примерно до десяти миллионов кельвинов, а затем вплоть до центра звезды почти не меняется.
Белые карлики хотя и слабо, но все-таки излучают. Что является источником энергии этого излучения? Как уже подчеркивалось выше, водорода, основного ядерного горючего, в недрах белых карликов практически нет. Он почти весь выгорел на стадиях эволюции звезды, предшествовавших стадии белого карлика. Но, с другой стороны, спектроскопические наблюдения с очевидностью указывают на то, что в самых наружных слоях белых карликов водород имеется. Он либо не успел выгореть, либо (что более вероятно) попал туда из межзвездной среды. Не исключено, что источником энергии белых карликов могут быть водородные ядерные реакции, происходящие в очень тонком сферическом слое на границе плотного вырожденного вещества их недр и атмосферы. Кроме того, белые карлики могут поддерживать довольно высокую температуру своей поверхности путем обычной теплопроводности. Это означает, что не имеющие источников энергии белые карлики остывают, излучая за счет запасов своего тепла. А эти запасы весьма солидны. Так как движения электронов в веществе белых карликов обусловлены явлением вырождения, запас тепла в их недрах содержится в ядрах и ионизованных атомах. Полагая, что вещество белых карликов состоит в основном из гелия (атомный вес равен 4), легко найти количество тепловой энергии, содержащейся в белом карлике:
где mH — масса атома водорода, k — постоянная Больцмана. Время охлаждения белого карлика можно оценить, поделив E T на его светимость L. Оно оказывается порядка нескольких сотен миллионов лет. На рис. 10.2 для ряда белых карликов приведена эмпирическая зависимость светимости от поверхностной температуры. Прямые линии суть геометрические места постоянных радиусов. Последние выражены в долях солнечного радиуса. Похоже на то, что эмпирические точки хорошо укладываются вдоль этих прямых. Это означает, что наблюдаемые белые карлики находятся на разных стадиях остывания. В последние годы для десятка белых карликов было обнаружено сильное расщепление спектральных линий поглощения, обусловленное эффектом Зеемана. Из величины расщепления следует, что напряженность магнитного поля на поверхности этих звезд достигает огромного значения порядка десяти миллионов эрстед (Э). Столь большое значение магнитного поля, по-видимому, объясняется условиями образования белых карликов. Например, если предположить, что без существенной потери массы звезда сжимается, можно ожидать, что магнитный поток (т. е. произведение площади поверхности звезды на напряженность магнитного поля) сохраняет свое значение. Отсюда следует, что напряженность магнитного поля по мере сжатия звезды будет расти обратно пропорционально квадрату ее радиуса. Следовательно, она может вырасти в сотни тысяч раз. Этот механизм увеличения магнитного поля особенно важен для нейтронных звезд, о чем будет идти речь в § 22[ 29 ]. Интересно отметить, что большинство белых карликов не имеет поля более сильного, чем несколько тысяч эрстед. Таким образом, «намагниченные» белые карлики образуют особую группу среди звезд этого типа. Глава 11 Модели звезд В § 6 мы получили основные характеристики звездных недр (температура, плотность, давление), используя метод грубых оценок величин, входящих в уравнения, описывающие состояния равновесия звезд. Хотя эти оценки дают правильное представление о физических условиях в центральных областях звезд, они, конечно, совершенно недостаточны для понимания сходства и различия между разными звездами. Например, для решения важного вопроса, какая именно ядерная реакция (протон-протонная или углеродно-азотная) ответственна за излучение той или иной конкретной звезды, необходимо более совершенное знание условий в ее недрах. Наконец, остается пока не рассмотренной основная задача: каков физический смысл диаграммы Герцшпрунга — Рессела? Эта задача, как мы увидим ниже, теснейшим образом связана с проблемой эволюции звезд. Хотя запасы ядерной энергии в недрах звезд очень велики, все же их нельзя считать неисчерпаемыми. Рано или поздно (в зависимости от массы звезды) они подойдут к концу. Что будет при этом происходить со звездой? Как она будет менять свои свойства? Чтобы понять связь между разными звездами и причины наблюдаемых различий между ними, надо хорошо знать мгновенное состояние разных звезд, как бы «моментальную фотографию» структуры их недр. Точно так же как реальные физические процессы можно представить как последовательность «квазистатических» состояний, очень медленный процесс эволюции звезды (обусловленный истощением запасов ее ядерного горючего) можно представить как последовательность ее равновесных конфигураций. Такие конфигурации, получаемые теоретическим, расчетным путем, носят название «звездных моделей». Под «звездной моделью» понимается совокупность таблиц (или графиков), дающих «идеализированное» распределение плотности, температуры, давления, химического состава вещества звезды для разных глубин, выраженных в долях ее радиуса. Следует подчеркнуть, что такая модель отнюдь не тождественна реальной звезде. Все же хорошо рассчитанная модель, правильно учитывающая основные физические законы, определяющие структуру звезды, может (и должна!) давать в основном верное представление о свойствах вещества звездных недр. Было бы ошибочно считать, что расчет звездных моделей содержит в себе элемент произвола. Наоборот, он непрерывно и жестко контролируется в процессе самих вычислений. И, наконец, он после своего завершения должен находиться в полном согласии с наблюдаемыми свойствами «моделируемых» звезд. Например, если речь идет о расчете модели звезды главной последовательности, у рассчитанной модели должно выполняться соотношение «масса — светимость». Если бы была возможность непосредственно наблюдать внутренние области звезд, не было бы надобности в построении их моделей. Ведь структуру туманностей, которые «видны насквозь», мы получаем непосредственно из оптических и радиоастрономических наблюдений. Увы, недра звезд скрыты от нас гигантской толщей звездного вещества и почти нет шансов «увидеть», что там происходит. Мы подчеркнули слово «почти», так как все-таки имеется одна возможность непосредственного наблюдения звездных недр, о которой было рассказано в § 9. Итак, построение звездных моделей есть процедура вынужденная, иначе мы не могли бы делать количественных выводов об основных тенденциях развития большей части вещества во Вселенной. Как же рассчитываются звездные модели? Прежде всего основой таких расчетов являются физические законы, определяющие равновесную конфигурацию звезды. Об этих законах уже шла речь в § 6 и 7. Это, во-первых, условие гидростатического равновесия, которое должно выполняться для каждого элемента объема внутри звезды (см. формулу (6.1)). Во-вторых,— так называемое «условие лучистого равновесия», описывающее перенос излучения из недр звезды, к ее поверхности (см. уравнение (7.10)). Далее необходимо учитывать, как меняется непрозрачность звездного вещества в зависимости от изменения температуры и плотности, а также зависимость давления от плотности и температуры, т. е. «уравнение состояния». Для вещества «нормальных» звезд последнее описывается уравнением Клапейрона, а для белых карликов — формулой (10.1). Необходимо учитывать и очень сильную зависимость скорости выделения ядерной энергии от температуры (см. стр. 246). Кроме того, считаются заданными такие основные параметры «моделируемых» звезд, как их масса, светимость и радиус. Ввиду сложности системы уравнений, описывающих состояние звезд, расчет модели не может быть сделан аналитически, т. е. по готовой, пусть даже очень громоздкой, формуле. Успех достигается только численным методом решения этих уравнений (являющихся, кстати, дифференциальными). Предполагается, что модель звезды сферически-симметричная, т. е. все характеристики какого-нибудь элемента ее объема (температура, плотность и пр.) зависят только от расстояния этого элемента от центра звезды. В чем же идея численного метода расчета? Представим себе, что звезда состоит из очень большого числа концентрических сферических слоев. В пределах каждого слоя (если он только выбран достаточно тонким) значения указанных характеристик можно считать постоянными. Зададим значения давления и температуры в центре звезды. Условия гидростатического равновесия позволят тогда найти давление на поверхности первой (самой внутренней) сферы. Далее, путем расчетов определяем, пользуясь формулой Клапейрона, температуру в центре. Затем, зная зависимость скорости ядерного энерговыделения от температуры и используя уравнение для переноса лучистой энергии (7.10), мы получим температуру на поверхности шаровой сферы, а затем, пользуясь формулой Клапейрона,— плотность. Такая процедура (как видим, довольно сложная!) позволяет по данным температуре, плотности и давлению в центре звезды получить те же основные характеристики на некотором относительно малом расстоянии от центра. После этого тем же методом процедура повторяется и получается значение характеристик звездного вещества, на поверхности второй сферы, радиус которой вдвое больше, чем у первой. Так, шаг за шагом, получается «разрез» всей звезды, т. е. значения основных характеристик ее вещества в зависимости от расстояния от центра. Для того чтобы расчет модели увенчался успехом, толщины воображаемых сфер, на которые разбивается звезда, должны быть достаточно малы. С другой стороны, конечно, непрактично делать их слишком маленькими, что привело бы к неоправданно большому увеличению объемов расчета. Практически количество таких сфер бывает порядка нескольких сотен, иногда даже нескольких тысяч. Масса рассчитанной модели получается как результат суммирования «парциальных» масс, заключенных в пределах элементарных сфер. Учитывая «производство» термоядерной энергии в разных слоях, можно по окончании расчета получить теоретическую светимость звездной модели. Раньше такие расчеты моделей выполнялись вручную, на арифмометрах. Однако последние три десятилетия расчеты моделей производятся преимущественно на электронных вычислительных машинах. Резкое увеличение «производительности труда», помимо облегчения работы вычислителя, позволило широко варьировать различные параметры, входящие в расчет, и выбирать из них те, которые дают разумные и непротиворечивые модели. В частности, условием непротиворечивости модели, дающей некоторые значения радиуса, массы и светимости звезды, является выполнение закона «масса — светимость», если речь идет о расчете модели звезды главной последовательности. Отчего же могут получиться в процессе расчетов модели, явно несоответствующие реальным звездам? В значительной степени это происходит из-за большой неуверенности в знании химического состава недр звезды, модель которой рассчитывается. Приходится при расчетах работать «методом проб и ошибок», отбрасывая такие предположения о химическом составе, которые приводят к явно несуразным результатам. Имеется и еще довольно специфическая причина расхождения между основными расчетными характеристиками модели звезды (т. е. ее массы, светимости и радиуса) и наблюдаемыми характеристиками соответствующей реальной звезды. Дело в том, что при некоторых условиях процесс переноса энергии в недрах звезды может менять свой характер. Например, перенос энергии путем лучеиспускания может смениться конвективным переносом. Это бывает по разным причинам. Так, если по мере погружения в глубину температура начинает расти довольно резко, лучеиспускание, возможности которого «ограничены», уже не в состоянии обеспечить транспортировку всей выделяющейся в недрах звезды энергии. Наступает неустойчивость, и доминирующим механизмом переноса энергии становится конвекция. Об этом речь шла уже в § 8. Поэтому в процессе вычислений, которые выполняются «шаг за шагом», следует внимательно следить и контролировать, как ведет себя механизм переноса энергии в строящейся модели звезды. Следует также иметь в виду, что химический состав звезды, определяемый параметрами X, Y , Z (см. § 7), не останется постоянным для всей звезды, а может систематически и притом радикально отличаться в ее разных частях. Например, в центральной области звезды, из-за «выгорания» водорода у сравнительно старых звезд, X может быть значительно меньше, чем на периферии. Модели звезд, учитывающие это обстоятельство, носят название «неоднородных». Такие модели представляют значительный интерес, так как хорошо отражают действительность. Приводя пример, как строится модель звезды, мы рассматривали такое построение идущим от центра к периферии. Можно и даже часто более удобно рассчитывать модель от поверхности к центру. В этом случае задаются радиус и светимость (или температура) звезды. Естественно, что по окончании расчета суммарная масса сферических слоев должна быть равна массе звезды. Неверные методы расчета могут привести к «исчерпанию» массы модели звезды задолго до того, как расчеты дойдут до центра. Автор когда-то наблюдал такой любопытный феномен в работах некоторых начинающих специалистов в области внутреннего строения звезд...
В результате большой работы, проделанной астрофизиками-теоретиками, специалистами по внутреннему строению звезд, в настоящее время имеется много моделей звезд. Эти модели охватывают звезды, занимающие различные места на диаграмме Герцшпрунга — Рессела. Мы сейчас обсудим основные особенности моделей, соответствующие звездному населению нашей Галактики. Прежде всего представляют интерес модели звезд главной последовательности на диаграмме Герцшпрунга — Рессела. Оказывается, что структура звезд верхней части этой последовательности (горячие массивные объекты высокой светимости) значительно отличается от структуры красных карликов, заполняющих ее нижнюю правую часть. На рис. 11.1 наглядно представлена структура массивной горячей звезды. Эта модель была рассчитана для звезды, масса которой в 10 раз больше солнечной, радиус в 3,6 раза больше, а светимость (болометрическая) в 3000 раз превосходит светимость Солнца. Это означает, что моделируемая звезда имеет спектральный класс В0, причем температура ее поверхности около 25 000 К. Как показывают расчеты, в центральной части звезды перенос энергии осуществляется путем конвекции. Радиус конвективной зоны составляет около 25% радиуса звезды. Эта зона содержит в себе также около 25% полной массы звезды. Характерна довольно большая концентрация плотности вещества по направлению к центру. В самом центре плотность примерно в 25 раз превосходит среднюю плотность звезды и близка к 7 г/см3. Центральная температура довольно высока — около 27 миллионов кельвинов, т. е. примерно в два раза больше, чем у Солнца. Качественно этого и следовало ожидать согласно простой формуле (6.2), хотя температура оказалась несколько ниже, чем рассчитанная по этой формуле. Модель не очень сильно зависит от принятого химического состава звезды (X = 0,90, Y = 0,09, Z = 0,01). Любопытно, в каком направлении будет меняться структура звезд такого типа, если уменьшать массу? Расчеты показывают, что при этом, во-первых, в соответствии с формулой (6.2) будет уменьшаться центральная температура, во-вторых, будут уменьшаться относительные размеры конвективного ядра. У таких звезд основным источником энергии является углеродно-азотная реакция. Как мы видели, скорость этой реакции очень сильно растет с ростом температуры (см. формулу (8.3)). Поэтому для «отвода» выделяющегося при этой реакции огромного количества энергии уже недостаточно одного лишь лучистого ее переноса. В этом случае транспортировку энергии берет на себя конвекция. Это и объясняет существование у таких звезд более или менее протяженных конвективных ядер в центральных областях. Схема на рис. 11.1 представляет структуру типичных звезд верхней части главной последовательности. На рис. 11.2 схематически представлена модель красного карлика с массой 0,6, светимостью 0,56 и радиусом 0,64 солнечного. Следовательно, речь идет о модели карликовой звезды спектрального класса К — М. Обращает на себя внимание то обстоятельство, что структура такой звезды значительно отличается от структуры массивных, горячих звезд верхней части главной последовательности. Прежде всего, в центральных частях карликовых звезд уже совсем нет конвективной зоны. Наоборот, в наружных слоях таких звезд перенос энергии осуществляется преимущественно путем конвекции. В приведенной на рис. 11.2 модели конвективная зона занимает наружную часть звезды, причем там сосредоточено примерно 10% ее массы. Причина отличия в структуре звезд нижней части главной последовательности от структуры массивных горячих звезд кроется в сравнительно низкой температуре недр карликовых звезд. Из-за этого растет непрозрачность звездного вещества и перенос вырабатываемой в центре звезды энергии путем излучения становится затруднительным. На помощь приходит конвекция. Концентрация вещества к центру у карликовых звезд не так велика, как у горячих гигантов. Центральная плотность уже только в 20 раз превосходит среднюю, хотя абсолютное значение центральной плотности гораздо выше, около 60 г/см3. В согласии с формулой (6.2) центральная температура в рассматриваемой модели карликовой звезды сравнительно низка — около 9 миллионов кельвинов. При такой температуре энергетика карликовых звезд обеспечивается только протон-протонной реакцией.
Солнце является довольно типичной звездой средней части главной последовательности. Вместе с тем модель внутреннего строения Солнца по понятным причинам представляет для нас особый интерес.
В последние годы было рассчитано несколько моделей Солнца, отличающихся численными значениями некоторых параметров расчета (прежде всего химического состава). Имеется еще одна важная особенность расчета моделей Солнца. Особенностью моделей звезд верхней и нижней частей главной последовательности, которые приведены на рис. 11.1 и 11.2, является их однородность. Это означает, что химический состав звезды предполагается постоянным во всем объеме звезды. Последнее предположение вполне естественно для карликовых звезд малой массы и сравнительно низкой светимости, время пребывания которых на главной последовательности превышает возраст Галактики. Поэтому в центральных частях этих звезд израсходована только малая часть первоначального «запаса» водородного «горючего». Что касается массивных звезд верхней части главной последовательности, то приведенная на рис. 11.1 модель относится к сравнительно молодым звездам этого типа. Иное дело Солнце. Возраст Солнца известен — около 5 миллиардов лет. За такой огромный срок уже можно ожидать некоторого уменьшения содержания водорода в центральной части нашего светила, так как заметная часть первоначального запаса водородного горючего Солнца уже израсходована— все-таки Солнце светит очень долго... Тут-то и кроется известная неопределенность в расчете модели Солнца, которая должна быть неоднородной. Какой процент солнечного водорода «выгорел» и в каком объеме? Ведь можно варьировать и объем, и процент «выгоревшего» водорода, что и делается в различных моделях. Любопытно, что центральная температура Солнца получается почти не зависящей от конкретных особенностей различных моделей. Она близка к 14 миллионам кельвинов — значению, которым мы пользовались в § 9. Это означает, что основной термоядерной реакцией в недрах Солнца является протон-протонная реакция, хотя небольшой вклад дает также углеродно-азотный цикл. Для модели, изображенной на рис. 11.3, принято, что в центральной области X = 0,50 и плавно растет до тех пор, пока на расстоянии от центра, равном 0,25 радиуса, становится равным около 75%, после чего, вплоть до самой поверхности, остается постоянным. Так же как и у красных карликов, у этой модели Солнца нет конвективного ядра, однако размеры наружной конвективной зоны значительно меньше. Заметим, что эта зона содержит всего около 2% массы Солнца. Центральная плотность Солнца довольно велика — она больше, чем у моделей звезд как верхней, так и нижней частей главной последовательности и равна 135 г/см3, что почти в 100 раз превосходит среднюю плотность. Такая большая концентрация массы к центру естественно объясняется частичным «выгоранием» водорода в центральных областях нашего светила. В сильнейшей степени этот эффект, как мы увидим, проявляется у красных гигантов. Развитие науки в нашу эпоху открыло совершенно неожиданную возможность уточнения модели Солнца, о чем уже шла речь в § 9. Специфической особенностью субкарликов является очень низкое содержание тяжелых элементов. Об этом уже говорилось в § 1. Поэтому при расчете моделей таких звезд величина Z полагается равной нулю. Так как содержание тяжелых элементов имеет решающее значение для непрозрачности звездного вещества, то при малом Z прозрачность вещества субкарликов должна быть очень высокой, даже если температура сравнительно низка. Поэтому лучеиспускание достаточно эффективно переносит энергию и нет необходимости в развитии конвекции. Центральная температура таких звезд довольно чувствительно зависит от принятого содержания гелия, которое толком не известно. Однако, пожалуй, самой интересной структурой обладают красные гиганты. На рис. 11.4 приведена модель довольно типичного красного гиганта, масса, радиус и светимость которого превосходят солнечные соответственно в 1,3, 21 и 225 раз. В самой центральной части звезды-гиганта находится маленькое ядро, температура которого очень высока — 40 миллионов кельвинов. В этом ядре практически нет водорода — он уже весь «выгорел», превратившись в гелий. Вместе с тем температура там еще недостаточно высока для «тройной» гелиевой реакции (см. § 8).
Из-за отсутствия источников энергии температура в области ядра постоянна. Поэтому такое ядро называется «изотермическим». Несмотря на очень малые размеры изотермического ядра (около одной тысячной радиуса звезды), в нем содержится примерно четверть всей массы звезды. Отсюда непосредственно следует, что плотность изотермического ядра огромна — порядка 3 Вокруг вырожденного изотермического ядра красного гиганта имеется очень тонкая оболочка, где происходят термоядерные реакции углеродно-азотного цикла. Толщина этой оболочки намного меньше радиуса изотермического ядра. В пределах этого тонкого слоя температура вещества резко падает от 40 до 25 миллионов кельвинов. Плотность вещества в оболочке уже в несколько тысяч раз меньше, чем в центре изотермического ядра. Оболочка, в которой происходят ядерные реакции, окружена в свою очередь сравнительно небольшой толщины (около 10% радиуса звезды) слоем, где выделяющаяся в описанном выше слое энергия переносится путем лучеиспускания. Основная же часть наружных слоев красного гиганта, содержащая почти 70% его массы и начинающаяся приблизительно на расстоянии 0,1 его радиуса от центра, находится в состоянии конвекции. Причина образования столь протяженной конвективной зоны — большая непрозрачность вещества — та же, что и у красных карликов. Таким образом, структура красных гигантов отличается крайней неоднородностью. В противоположность очень сложной структуре красных гигантов структура белых карликов отличается большой простотой. Об этой структуре речь уже шла в § 10. В двух словах: белый карлик— это очень плотный газовый шар, электроны которого вырождены, окруженный сравнительно тонкой оболочкой, из «обычного» газа (рис. 11.5). Парадоксальность ситуации, однако, состоит в том, что, казалось бы столь различные объекты, как красные гиганты и белые карлики, генетически связаны между собой. Об этом речь будет идти в § 13. Глава 12 Эволюция звезд Как уже подчеркивалось в § 6, подавляющее большинство звезд меняет свои основные характеристики (светимость, радиус) очень медленно. В каждый данный момент их можно рассматривать как находящиеся в состоянии равновесия — обстоятельство, которым мы широко пользовались для выяснения природы звездных недр. Но медленность изменений — это еще не означает отсутствие их. Все дело в сроках эволюции, которая для звезд должна быть совершенно неизбежной. В самом общем виде задача об эволюции какой-нибудь звезды может быть поставлена следующим образом. Допустим, что имеется звезда с данной массой и радиусом. Кроме того, известен ее первоначальный химический состав, который будем считать постоянным по всему объему звезды. Тогда ее светимость следует из расчета модели звезды. В процессе эволюции химический состав звезды неизбежно должен меняться, так как из-за поддерживающих ее светимость термоядерных реакций содержание водорода необратимо уменьшается со временем. Кроме того, химический состав звезды перестанет быть однородным. Если в ее центральной части процентное содержание водорода заметно уменьшится, то на периферии оно останется практически неизменным. Но это означает, что по мере эволюции звезды, связанной с «выгоранием» ее ядерного горючего, должна меняться сама модель звезды, а следовательно, ее структура. Следует ожидать изменения светимости, радиуса, поверхностной температуры. Как следствие таких серьезных изменений, звезда постепенно будет менять свое место на диаграмме Герцшпрунга — Рессела. Следует себе представить, что она на данной диаграмме опишет некую траекторию или, как принято говорить, «трек». Проблема эволюции звезд, несомненно, принадлежит к числу фундаментальнейших проблем астрономии. По существу, вопрос заключается в том, как рождаются, живут, «стареют» и умирают звезды. Именно этой проблеме посвящена настоящая книга. Эта проблема по самой своей сущности является комплексной. Она решается целеустремленными исследованиями представителей разных отраслей астрономии — наблюдателей и теоретиков. Ведь изучая звезды, никак нельзя сразу сказать, какие из них находятся в генетическом родстве. Вообще эта проблема оказалась очень трудной и несколько десятилетий совершенно не поддавалась решению. Более того, вплоть до сравнительно недавнего времени усилия исследователей зачастую шли в совершенно ложном направлении. Так, например, само наличие главной последовательности на диаграмме Герцшпрунга — Рессела «вдохновило» многих наивных исследователей на представление, что звезды эволюционируют вдоль этой диаграммы от горячих голубых гигантов до красных карликов. Но так как существует соотношение «масса — светимость», согласно которому масса звезд, расположенных вдоль главной последовательности, должна непрерывно убывать, упомянутые исследователи упорно считали, что эволюция звезд в указанном направлении должна сопровождаться непрерывной и притом весьма значительной потерей их массы. Все это оказалось неверным. Постепенно вопрос о путях эволюции звезд прояснился, хотя отдельные детали проблемы все еще далеки от решения. Особая заслуга в понимании процесса эволюции звезд принадлежит астрофизикам-теоретикам, специалистам по внутреннему строению звезд и прежде всего американскому ученому М. Шварцшильду и его школе. Ранний этап эволюции звезд, связанный с процессом их конденсации из межзвездной среды, был рассмотрен в конце первой части этой книги. Там, собственно говоря, речь шла даже не о звездах, а о протозвездах. Последние, непрерывно сжимаясь под действием силы тяжести, становятся все более компактными объектами. Температура их недр при этом непрерывно растет (см. формулу (6.2)), пока не станет порядка нескольких миллионов кельвинов. При такой температуре в центральных областях протозвезд «включаются» первые термоядерные реакции на легких ядрах (дейтерий, литий, бериллий, бор), у которых «кулоновский барьер» сравнительно низок. Когда пойдут эти реакции, сжатие протозвезды замедлится. Однако довольно быстро легкие ядра «выгорят», так как их обилие невелико, и сжатие протозвезды будет продолжаться почти с прежней скоростью (см. уравнение (3.6) в первой части книги), протозвезда «стабилизуется», т. е. перестанет сжиматься, только после того как температура в ее центральной части поднимется настолько, что «включатся» протон-протонная или углеродно-азотная реакции. Она примет равновесную конфигурацию под действием сил собственной гравитации и перепада газового давления, которые практически точно скомпенсируют друг друга (см. § 6). Собственно говоря, с этого момента протозвезда и становится звездой. Молодая звезда «садится» на свое место где-то на главной последовательности. Точное ее место на главной последовательности определяется значением первоначальной массы протозвезды. Массивные протозвезды «садятся» на верхнюю часть этой последовательности, протозвезды со сравнительно небольшой массой (меньше солнечной) «садятся» на ее нижнюю часть. Таким образом, протозвезды непрерывно «входят» в главную последовательность на всем ее протяжении, так сказать, «широким фронтом». «Протозвездная» стадия эволюции звезд довольно быстротечна. Самые массивные звезды проходят эту стадию всего лишь за несколько сотен тысяч лет. Неудивительно поэтому, что число таких звезд в Галактике невелико. Поэтому не так-то просто их наблюдать, особенно если учесть, что места, где происходит процесс звездообразования, как правило, погружены в поглощающие свет пылевые облака. Зато после того как они «пропишутся на своей постоянной площади» на главной последовательности диаграммы Герцшпрунга — Рессела, ситуация резко изменится. В течение весьма длительного времени они будут находиться на этой части диаграммы, почти не меняя своих свойств. Поэтому основная часть звезд наблюдается на указанной последовательности. Структура моделей звезды, когда она еще сравнительно недавно «села» на главную последовательность, определяется моделью, вычисленной в предположении, что ее химический состав одинаков во всем объеме («однородная модель»; см. рис. 11.1, 11.2). По мере «выгорания» водорода состояние звезды будет очень медленно, но неуклонно меняться, вследствие чего изображающая звезду точка будет описывать некоторый «трек» на диаграмме Герцшпрунга — Рессела. Характер изменения состояния звезды существенным образом зависит от того, перемешивается ли вещество в ее недрах или нет. Во втором случае, как мы видели для некоторых моделей в предыдущем параграфе, в центральной области звезды обилие водорода становится из-за ядерных реакций заметно меньшим, чем на периферии. Такая звезда может описываться только неоднородной моделью. Но возможен и другой путь звездной эволюции: перемешивание происходит во всем объеме звезды, которая по этой причине всегда сохраняет «однородный» химический состав, хотя содержание водорода со временем будет непрерывно уменьшаться. Заранее сказать, какая из этих возможностей реализуется в природе, было невозможно. Конечно, в конвективных зонах звезд всегда идет интенсивный процесс перемешивания вещества и в пределах этих зон химический состав должен быть постоянен. Но и для тех областей звезд, где доминирует перенос энергии путем лучеиспускания, перемешивание вещества также вполне возможно. Ведь никогда нельзя исключить систематических довольно медленных движений больших масс вещества с небольшими скоростями, которые приведут к перемешиванию. Такие движения могут возникнуть из-за некоторых особенностей вращения звезды. Вычисленные модели какой-нибудь звезды, у которой при постоянной массе систематически меняется как химический состав, так и мера неоднородности, образуют так называемую «эволюционную последовательность». Нанося на диаграмму Герцшпрунга — Рессела точки, соответствующие разным моделям эволюционной последовательности звезды, можно получить ее теоретический трек на этой диаграмме. Оказывается, что если бы эволюция звезды сопровождалась полным перемешиванием ее вещества, треки были бы направлены от главной последовательности влево. Наоборот, теоретические эволюционные треки для неоднородных моделей (т. е. при отсутствии полного перемешивания) всегда уводят звезду направо от главной последовательности. Какой же из двух теоретически вычисленных путей звездной эволюции правильный? Как известно, критерий истины есть практика. В астрономии практика,— это результаты наблюдений. Посмотрим на диаграмму Герцшпрунга — Рессела для звездных скоплений, изображенную на рис. 1.6, 1.7 и 1.8. Мы там не найдем звезд, расположенных вверху и слева от главной последовательности. Зато имеется очень много звезд справа от нее — это красные гиганты и субгиганты. Следовательно, такие звезды мы можем рассматривать как покидающие главную последовательность в процессе своей эволюции, не сопровождающейся полным перемешиванием вещества в их недрах. Объяснение природы красных гигантов — одно из крупнейших достижений теории эволюции звезд[ 30 ]. Сам по себе факт существования красных гигантов означает, что эволюция звезд, как правило, не сопровождается перемешиванием вещества во всем их объеме. Расчеты показывают, что по мере эволюции звезды размеры и масса ее конвективного ядра непрерывно уменьшаются[ 31 ]. Очевидно, что сама по себе эволюционная последовательность моделей звезды еще ничего не говорит о темпах звездной эволюции. Временная шкала эволюции может быть получена из анализа изменения химического состава у разных членов эволюционной последовательности моделей звезды. Можно определить некоторое среднее содержание водорода в звезде, «взвешенное» по ее объему. Обозначим это среднее содержание через X. Тогда, очевидно, изменение со временем величины X определяет светимость звезды, так как она пропорциональна количеству термоядерной энергии, выделившейся в звезде за одну секунду. Поэтому можно написать:
где
где X0 — начальное обилие водорода в звезде, когда она только «села» на главную последовательность. Для незнакомых с высшей математикой читателей можно написать упрощенное выражение для промежутка времени, прошедшего между двумя состояниями . звезды с разными, хотя и мало отличающимися значениями X:
Суммируя промежутки времени
На рис. 12.1 приведены теоретически рассчитанные эволюционные треки для сравнительно массивных звезд. Начинают они свою эволюцию на нижней кромке главной последовательности. По мере выгорания водорода такие звезды перемещаются по своим трекам в общем направлении поперек главной последовательности, не выходя за ее пределы (т. е. оставаясь в пределах ее ширины). Этот этап эволюции, связанный с пребыванием звезд на главной последовательности, является самым длительным. Когда содержание водорода в ядре такой звезды станет близким к 1%, темпы эволюции ускорятся. Для поддержания энерговыделения на необходимом уровне при резко уменьшившемся содержании водородного «топлива» необходимо в качестве «компенсации» увеличение температуры ядра. И здесь, как и во многих других случаях, звезда сама регулирует свою структуру (см. § 6). Увеличение температуры ядра достигается путем сжатия звезды как целого. По этой причине эволюционные треки круто поворачивают налево, т. е. температура поверхности звезды возрастает. Очень скоро, однако, сжатие звезды прекращается, так как весь водород в ядре выгорает. Зато «включается» новая область ядерных реакций — тонкая оболочка вокруг уже «мертвого» (хотя и очень горячего) ядра. По мере дальнейшей эволюции звезды эта оболочка все дальше и дальше отходит от центра звезды, тем самым увеличивая массу «выгоревшего» гелиевого ядра. Одновременно будет происходить процесс сжатия этого ядра и его разогрев. Однако при этом наружные слои такой звезды начинают быстро и очень сильно «разбухать». Это означает, что при мало изменяющемся потоке поверхностная температура значительно уменьшается. Ее эволюционный трек круто поворачивает направо и звезда приобретает все признаки красного сверхгиганта. Так как к такому состоянию звезда после прекращения сжатия приближается довольно быстро, почти нет звезд, заполняющих на диаграмме Герцшпрунга — Рессела разрыв между главной последовательностью и ветвью гигантов и сверхгигантов. Это хорошо видно на таких диаграммах, построенных для открытых скоплений (см. рис. 1.8). Дальнейшая судьба красных сверхгигантов еще недостаточно хорошо изучена. К этому важному вопросу мы вернемся в следующем параграфе. Разогрев ядра может происходить вплоть до очень высоких температур, порядка сотни миллионов кельвинов. При таких температурах «включается» тройная гелиевая реакция (см. § 8). Выделяющаяся при этой реакции энергия останавливает дальнейшее сжатие ядра. После этого ядро слегка расширится, а радиус звезды уменьшится. Звезда станет горячее и сдвинется влево на диаграмме Герцшпрунга — Рессела. Несколько иначе протекает эволюция у звезд с меньшей массой, например, M На рис. 12.2 приведен эволюционный трек звезды с массой, равной 5M
Из простого рассмотрения эволюционных треков, изображенных на рис. 12.3, следует, что более или менее массивные звезды довольно «извилистым» путем уходят с главной последовательности, образуя ветвь гигантов на диаграмме Герцшпрунга — Рессела. Характерен очень быстрый рост светимости звезд с меньшей массой по мере их эволюции в направлении красных гигантов. Разница в эволюции таких звезд по сравнению с более массивными состоит в том, что у первых образуется очень плотное, вырожденное ядро. Такое ядро, из-за большого давления вырожденного газа (см. § 10), способно «удерживать» вес лежащих выше слоев звезды. Оно почти не будет сжиматься, а следовательно, сильно нагреваться. Поэтому «тройная» гелиевая реакция если и включится, то гораздо позже. За исключением физических условий, в области около центра структура таких звезд будет похожа на структуру более массивных. Следовательно, их эволюция после выгорания водорода в центральной области также будет сопровождаться «разбуханием» наружной оболочки, что приведет их треки в область красных гигантов. Однако в отличие от более массивных сверхгигантов, их ядра будут состоять из весьма плотного вырожденного газа (см. схему на рис. 11.4).
Пожалуй, наиболее выдающимся достижением развитой в этом параграфе теории звездной эволюции является объяснение ею всех особенностей диаграммы Герцшпрунга — Рессела для скоплений звезд. Описание этих диаграмм было уже дано в § 1. Как уже говорилось в указанном параграфе, возраст всех звезд в данном скоплении следует считать одинаковым. Так же одинаковым должен быть первоначальный химический состав этих звезд. Ведь все они образовались из одного и того же (правда, достаточно крупного) агрегата межзвездной среды — газово-пылевого комплекса. Различные звездные скопления должны отличаться друг от друга прежде всего возрастом и, кроме того, первоначальный химический состав шаровых скоплений должен резко отличаться от состава рассеянных скоплений.
Линии, вдоль которых на диаграмме Герцшпрунга — Рессела располагаются звезды скоплений, никоим образом не означают их эволюционные треки. Эти линии суть геометрическое место точек на указанной диаграмме, где звезды с различными массами имеют одинаковый возраст. Если мы хотим сравнить теорию звездной эволюции с результатами наблюдений, прежде всего следует построить теоретически «линии одинакового возраста» для звезд с различными массами и одинаковым химическим составом. Возраст звезды на различных этапах ее эволюции можно определить, воспользовавшись формулой (12.3). При этом необходимо пользоваться теоретическими треками звездной эволюции типа тех, которые изображены на рис. 12.3. На рис. 12.4 приведены результаты вычислений для восьми звезд, массы которых меняются в пределах от 5,6 до 2,5 солнечной массы. На эволюционных треках каждой из этих звезд отмечены точками положения, которые соответствующие звезды займут через сто, двести, четыреста и восемьсот миллионов лет своей эволюции от первоначального состояния на нижней кромке главной последовательности. Кривые, проходящие через соответствующие точки для различных звезд, и есть «кривые одинакового возраста». В нашем случае расчеты велись для достаточно массивных звезд. Рассчитанные промежутки времени их эволюции охватывают по крайней мере 75% срока их «активной жизни», когда они излучают вырабатываемую в их недрах термоядерную энергию. Для самых массивных звезд эволюция доходит до стадии вторичного сжатия, наступающего после полного выгорания водорода в их центральных частях. Если сравнить полученную теоретическую кривую равного возраста с диаграммой Герцшпрунга — Рессела для молодых звездных скоплений (см. рис. 12.5, а также 1.6), то невольно бросается в глаза ее поразительное сходство с основной линией этого скопления. В полном соответствии с главным положением теории эволюции, согласно которому более массивные звезды быстрее уходят с главной последовательности, диаграмма на рис. 12.5 ясно указывает, что верхняя часть этой последовательности звезд в скоплении загибается вправо. Место главной последовательности, где звезды начинают заметно от нее отклоняться, находится тем «ниже», чем больше возраст скопления. Уже одно это обстоятельство позволяет непосредственно сравнивать возраст различных звездных скоплений. У старых скоплений главная последовательность обрывается сверху где-то около спектрального класса А. У молодых скоплений пока еще «цела» вся главная последовательность, вплоть до горячих массивных звезд спектрального класса В. Например, такая ситуация видна на диаграмме для скопления NGC 2264 (рис. 1.6). И действительно, вычисленная для этого скопления линия одинакового возраста Дает срок его эволюции всего лишь в 10 миллионов лет. Таким образом, это скопление родилось «на памяти» древних предков человека — рамапитеков... Значительно более старое скопление звезд — Плеяды, диаграмма которого изображена на рис. 1.4, имеет вполне «средний» возраст около 100 миллионов лет. Там еще сохранились звезды спектрального класса В7. А вот скопление в Гиадах (см. рис. 1.5) довольно старенькое — его возраст около одного миллиарда лет, и поэтому главная последовательность начинается только со звезд класса А. Теория эволюции звезд объясняет еще одну любопытную особенность диаграммы Герцшпрунга — Рессела для «молодых» скоплений. Дело в том, что сроки эволюции для маломассивных карликовых звезд очень велики. Например, многие из них за 10 миллионов лет (срок эволюции скопления NGC 2264) еще не прошли стадию гравитационного сжатия и, строго говоря, являются даже не звездами, а протозвездами. Такие объекты, как мы знаем, располагаются справа от диаграммы Герцшпрунга — Рессела (см. рис. 5.2, где эволюционные треки звезд начинаются на ранней стадии гравитационного сжатия). Если поэтому у молодого скопления карликовые звезды еще «не сели» на главную последовательность, нижняя часть последней будет у такого скопления смещена вправо, что и наблюдается (см. рис. 1.6). Наше Солнце, как мы уже говорили выше, несмотря на то, что оно уже «исчерпало» заметную часть своих «водородных ресурсов», еще не вышло из полосы главной последовательности диаграммы Герцшпрунга — Рессела, хотя оно и эволюционирует около 5 миллиардов лет. Расчеты показывают, что «молодое», недавно «севшее» на главную последовательность Солнце излучало на 40% меньше, чем сейчас, причем его радиус был всего лишь на 4% меньше современного, а температура поверхности равнялась 5200 К (сейчас 5700 К).
Теория эволюции непринужденно объясняет особенности диаграммы Герцшпрунга — Рессела для шаровых скоплений. Прежде всего это очень старые объекты. Их возраст лишь ненамного меньше возраста Галактики. Это ясно следует из почти полного отсутствия на этих диаграммах звезд верхней части главной последовательности. Нижняя часть главной последовательности, как уже говорилось в § 1, состоит из субкарликов. Из спектроскопических наблюдений известно, что субкарлики очень бедны тяжелыми элементами — их там может быть в десятки раз меньше, чем у «обычных» карликов. Поэтому первоначальный химический состав шаровых скоплений существенно отличался от состава вещества, из которого образовались рассеянные скопления: там было слишком мало тяжелых элементов. На рис. 12.6 представлены теоретические эволюционные треки звезд с массой 1,2 солнечной (это близко к массе звезды, которая успела проэволюционировать за 6 миллиардов лет), но с разным первоначальным химическим составом. Отчетливо видно, что после того как звезда «сошла» с главной последовательности, светимость для одинаковых фаз эволюции при малом содержании металлов будет значительно выше. Одновременно эффективные температуры поверхности у таких звезд будут выше. На рис. 12.7 показаны эволюционные треки маломассивных звезд с малым содержанием тяжелых элементов. На этих кривых точками указаны положения звезд после шести миллиардов лет эволюции. Соединяющая эти точки более жирная линия, очевидно, есть линия одинакового возраста. Если сравнить эту линию с диаграммой Герцшпрунга — Рессела для шарового скопления М 3 (см. рис. 1.8), то сразу же бросается в глаза полное совпадение этой линии с линией, по которой «уходят» с главной последовательности звезды этого скопления.
На приведенной на рис. 1.8 диаграмме видна также горизонтальная ветвь, отклоняющаяся от последовательности гигантов налево. По-видимому, она соответствует звездам, в недрах которых идет «тройная» гелиевая реакция (см. § 8). Таким образом, теория эволюции звезд объясняет все особенности диаграммы Герцшпрунга — Рессела для шаровых скоплений их «древним возрастам» и малым обилием тяжелых элементов[ 32 ]. Очень любопытно, что у скопления в Гиадах наблюдается несколько белых карликов, а в Плеядах — нет. Оба скопления сравнительно близки к нам, поэтому различными «условиями видимости» это интересное различие между двумя скоплениями объяснить нельзя. Но мы уже знаем, что белые карлики образуются на заключительной стадии красных гигантов, массы которых сравнительно невелики. Поэтому для полной эволюции такого гиганта необходимо немалое время — по крайней мере миллиард лет. Это время «прошло» у скопления в Гиадах, но «еще не наступило» в Плеядах. Именно поэтому в первом скоплении есть уже некоторое количество белых карликов, а во втором — нет. На рис. 12.8 представлена сводная схематическая диаграмма Герцшпрунга — Рессела для ряда скоплений, рассеянных и шаровых. На этой диаграмме эффект различия возрастов у разных скоплений виден вполне отчетливо. Таким образом, имеются все основания утверждать, что современная теория строения звезд и основанная на ней теория звездной эволюции смогли непринужденно объяснить основные результаты астрономических наблюдений. Несомненно, это является одним из наиболее выдающихся достижений астрономии XX столетия. Глава 13 Планетарные туманности, белые карлики и красные гиганты На последних этапах эволюции красных гигантов (так же как и сверхгигантов) становится существенной потеря массы наружной оболочкой. Этот заключительный этап эволюции очень трудно рассчитывать теоретически ввиду большой его неопределенности. Ведь мы не знаем точно, как осуществляется выбрасывание вещества из оболочек таких звезд. Приходится пока ограничиться качественным рассмотрением. На всех предыдущих этапах звездной эволюции (гравитационное сжатие протозвезды, пребывание на главной последовательности и уход с нее после исчерпания запасов ядерного горючего в центральных областях) предполагалось, что сколько-нибудь существенной потери массы не происходит. Следует, правда, заметить, что у массивных горячих звезд главной последовательности, как показывают последние спектроскопические наблюдения, выполненные в ультрафиолетовых лучах с ракет и спутников, имеет место довольно значительная потеря массы. Но это другой вопрос. Что касается красных гигантов, то чисто эмпирические аргументы говорят о том, что они прекращают свое существование как звезды отнюдь не из-за исчерпания ядерного горючего, а просто по причине потери своих наружных, богатых водородом оболочек. Мы сейчас укажем на один простой аргумент, который был предложен автором этой книги еще в 1956 г. Речь идет о давно известном астрономам феномене, называемом «планетарными туманностями». Это довольно плотные газовые образования, окружающие некоторые весьма горячие звезды низкой светимости. Фотографии двух планетарных туманностей приведены на рис. 13.1. На протяжении нескольких десятилетий эти туманности рассматривались астрономами как природная лаборатория, в которой с большим успехом можно изучать специфические физические процессы, протекающие в межзвездной среде. Изучение планетарных туманностей обогатило астроспектроскопию рядом открытий первостепенной важности. Стоит упомянуть хотя бы об изучении очень интересного процесса флуоресценции атомов под воздействием жесткого излучения, исследовании «запрещенных» переходов линий ионизованных кислорода и азота и др. Именно для планетарных туманностей с большой точностью был определен химический состав, что имеет исключительно большое значение для всей астрономии. Однако такой неизбежно «утилитарный» подход к этим поразительным объектам оставлял без внимания главное: откуда они взялись? Каково их происхождение? Следует заметить, правда, что недостатка в гипотезах не было, но все они были по своему характеру весьма произвольны и искусственны.
При подходе к решению проблемы планетарных туманностей я обратил внимание на основное, с моей точки зрения, обстоятельство. А именно, газ, образующий туманность, не сдерживается силой притяжения, поэтому эти объекты должны неограниченно расширяться со сравнительно небольшой скоростью и довольно быстро, всего лишь за несколько десятков тысяч лет, рассеяться в межзвездном пространстве. В процессе такого расширения плотность газа будет быстро падать. Еще быстрее должна поэтому падать светимость планетарных туманностей, так как излучение их единицы объема, обусловленное столкновениями электронов с ионами, пропорционально квадрату плотности газа. Как же выглядят эти объекты, когда они еще совсем «молодые», т. е. их возраст порядка нескольких тысяч лет? Анализ показал, что такие «сверхмолодые» туманности, «только что» отделившиеся каким-то образом от своих центральных звезд, во-первых, имеют крайне малые размеры, всего лишь в несколько тысяч астрономических единиц, во-вторых, они достаточно плотны, а в-третьих, и это самое интересное,— их наружные слои должны представлять собой сравнительно холодный неионизованный газ. В то же время светимость таких сверхмолодых туманностей примерно в тысячу раз больше солнечной. Разумеется, никакой центральной горячей звезды (вроде изображенных на рис. 13.1) за толстым слоем газа уже не видно. На что же похож такой странный объект? Нетрудно убедиться, что он по всем своим основным свойствам совпадает с протяженной, холодной атмосферой красного гиганта. Важным дополнительным подтверждением основного вывода, что планетарные туманности — это наружные слои красных гигантских звезд, утратившие связь с более внутренними горячими областями, в которых сосредоточена большая часть первоначальной массы звезды, является анализ пространственного распределения этих объектов. Оказывается, планетарные туманности сравнительно слабо концентрируются к галактической плоскости и обнаруживают значительную концентрацию к центру нашей звездной системы. Уже одно это указывает, что эти туманности являются конечным продуктом длительной эволюции очень старых звезд галактического диска. Точно такое же пространственное распределение имеют и некоторые красные гиганты высокой светимости. При такой интерпретации планетарных туманностей с необходимостью следует естественный вывод, что очень горячие ядра планетарных туманностей — это «обнажившиеся» недра красного гиганта. Такое «обнажение» произошло после того, как наружные слои красного гиганта по каким-то причинам потеряли с ним связь и, медленно расширяясь, «расползлись» по достаточно большому объему. Заметим, что по моей оценке, ныне являющейся общепризнанной, средняя масса планетарной туманности равна около 0,2 солнечной. А теперь представим себе, как бы выглядела звезда — красный гигант с массой чуть больше солнечной, если бы «вдруг» она лишилась своей столь «мощной» сравнительно холодной «шубы». Это был бы очень маленький объект с весьма высокой температурой, наружные слои которого находятся в состоянии бурной конвекции (см. схему модели на рис. 11.2). Из расчета модели красного гиганта следует, что плотность вещества на. уровне, выше которого имеется 0,2 массы Солнца, порядка 10-4 г/см3, что в сотню раз больше, чем в солнечной фотосфере. На этом уровне температура будет около 200 000 К, в то время как радиус этого слоя примерно в десять раз превышает радиус Солнца. По-видимому, одновременно с отделением наружных слоев красного гиганта происходит довольно быстрое (но не катастрофическое) сжатие его внутренних областей до размеров лишь в несколько раз превышающих размеры земного шара. Впрочем, вполне возможно, что красные гиганты типа RV Тельца, по-видимому, являющиеся «родителями» планетарных туманностей имеют на заключительной стадии своей эволюции структуру, отличную от описанной выше. Например, у них может быть гораздо более сильная концентрация вещества к центру. Необходимо подчеркнуть, что отделение наружных оболочек от основного «тела» звезды не носит взрывной характер (как это имеет место, например, в случае сверхновых звезд; см. следующую главу), а происходит спокойно, практически «с нулевой скоростью». Какова же причина отделения оболочки? Следует заметить, что задача эта еще очень далека от решения. Возможные варианты будут рассмотрены ниже. Образовавшийся после отделения наружной оболочки очень горячий объект должен быть в неустойчивом «промежуточном» состоянии. Он будет быстро эволюционировать, переходя в некоторое стабильное состояние. Что же это за состояние? Не подлежит сомнению, что таким стабильным объектом, в который эволюционируют ядра планетарных туманностей, должны быть белые карлики. Для отдельных ядер этот вывод следует непосредственно. Например, очень слабое ядро изображенной на рис. 13.1 планетарной туманности NGC 7293 (кстати, это самый близкий к нам объект этого типа) имеет абсолютную величину 13,5 и температуру больше 100 000 К. Отсюда следует, что его линейные размеры лишь немногим превышают размеры земного шара, что при массе около 1 массы Солнца дает среднюю плотность в несколько сотен тысяч граммов на кубический сантиметр. Это типичная плотность белого карлика! Наблюдается также любопытная тенденция: чем «старше» планетарная туманность (а их возраст оценить довольно легко), тем больше их ядра походят на белые карлики. Похоже на то, что за сравнительно короткое время, которое «живут» планетарные туманности, их ядра далеко не всегда успевают «успокоиться» и стать более или менее «нормальными» белыми карликами. Важнейшим аргументом в пользу нашего вывода о генетической связи планетарных туманностей, красных гигантов и белых карликов является анализ статистических данных. Всего в нашей Галактике одновременно существуют несколько десятков тысяч планетарных туманностей, причем только малая их часть доступна прямым наблюдениям. С другой стороны, среднее время жизни их всего лишь порядка нескольких десятков тысяч лет. Это означает, что из какого-то источника каждый год возникает примерно одна планетарная туманность. И как «побочный продукт» появляется ежегодно точно такое же количество белых карликов — конечный продукт эволюции ядер этих туманностей. Это очень эффективный механизм, который за время эволюции нашей звездной системы привел к образованию нескольких миллиардов белых карликов. Но именно таков порядок величины полного количества белых карликов в Галактике! С другой стороны, статистика красных гигантов типа RV Тельца указывает, что их полное количество в Галактике около миллиона. Отсюда получается, что если считать их «родителями» планетарных туманностей, то время жизни звезд в этой стадии около миллиона лет — величина вполне приемлемая. В § 11 уже было обращено внимание на то, что вещество самых центральных областей красных гигантов по своим свойствам (вырождение!) тождественно веществу белых карликов. Сейчас мы видим, что это не случайное совпадение. Подобно яйцу в курице, белый карлик постепенно вызревает в центре звезды с тем, чтобы «в подходящий момент» «вылупиться». Новорожденный «цыпленок», т. е. белый карлик, окружен разного рода «скорлупой» и прочими атрибутами своего рождения. Мы его называем «ядром планетарной туманности». Проходит, однако, несколько десятков или сотен тысяч лет — и получается нормальный белый карлик, в то время как образовавшаяся одновременно с ним планетарная туманность уже давно рассеялась в межзвездном пространстве. Нарисованная только что качественная картина заключительной фазы эволюции красных гигантов к одновременному образованию планетарных туманностей и их ядер — маленьких, плотных горячих звезд, быстро эволюционирующих в белые карлики,— в последние годы получила большое развитие в ряде работ, опирающихся на достижения теории звездной эволюции. Сейчас уже многие детали этого важнейшего для звездной космогонии процесса стали ясными.
Прежде всего следует более подробно остановиться на процессе эволюции ядра планетарной туманности в белый карлик. В свое время (1956 г.) автор этой книги обратил внимание на то, что в процессе быстрой эволюции ядер температуры их поверхностных слоев вначале растут. Так как при этом светимости меняются не очень-то сильно, то можно было сделать вывод, что ядра быстро сжимаются. Более точные теоретические расчеты, опирающиеся на наблюдения планетарных туманностей в Магеллановых Облаках[ 33 ], привели к установлению эмпирической зависимости между светимостью ядер планетарных туманностей и температурой их поверхностных слоев Te. Эта зависимость схематически представлена на рис. 13.2. На том же рисунке прерывистой линией показана аналогичная зависимость для остывающих белых карликов. Там же приведена зависимость «светимость — температура» для звезд главной последовательности, красных гигантов и так называемой «горизонтальной ветви» диаграммы Герцшпрунга — Рессела для шаровых скоплений. Уменьшение светимости ядер планетарных туманностей после достижения максимума при росте температуры означает их быстрое сжатие. В области диаграммы между самыми горячими ядрами и белыми карликами также наблюдаются слабые звезды. В их спектрах отсутствуют линии излучения и поглощения и очень усилена фиолетовая часть. Почти наверняка это сильно проэволюционировавшие ядра планетарных туманностей, у которых сами туманности, по причине их расширения, рассеялись. Таким образом, диаграмма «светимость — температура» наглядно демонстрирует (притом чисто эмпирически!) генетическую связь ядер планетарных туманностей и белых карликов.
Основы теории такой эволюции могут быть поняты из следующих рассуждений. Рассмотрим однородную по своему химическому составу звезду, которая, исчерпав свои ядерные источники энергии, сжимается за характерное время, определяемое шкалой Кельвина (см. § 3). При этом плотность вещества в ее центре будет расти по закону R-3. Теоретический расчет эволюции такой идеализированной звезды позволяет найти ее болометрическую светимость, центральную температуру, а также температуру поверхности как функции центральной плотности. Кроме того, можно теоретически получить зависимость L — Te. Соответствующие кривые см. на рис. 13.3. Мы видим, что зависимость L — Te для такой модели хорошо представляет эмпирическую зависимость, приведенную на рис. 13.2. Были выполнены также детальные расчеты для более сложных моделей звезд, лишенных ядерных источников (например, при очень высоких центральных температурах следует учитывать процессы образования большого количества нейтрино, свободно уносящих энергию из недр звезды). На рис. 13.4 приведена вычисленная зависимость L — Te для модели звезды с массой 1,02 солнечной, состоящей целиком из однородной смеси углерода и кислорода. Модель, в которой 5% вещества звезды образуют наружную оболочку, состоящую из гелия, сильно меняет рассчитанную кривую (см. рис. 13.4). Все же в широких пределах изменений параметров модели характер зависимости болометрической светимости от поверхностной температуры меняется мало и соответствует эмпирической диаграмме, приведенной на рис. 13.2.
При каких же условиях предположение о том, что звезда эволюционирует без ядерных источников, выполняется? Энерговыделение при ядерных реакциях прежде всего зависит от температуры и притом очень сильно. Следовательно, условием того, что ядерные реакции «не работают», является сравнительная малость центральной температуры. Чем же определяется эта верхняя граница температуры звездных недр? Прежде всего их химическим составом. Если, например, центральная температура равна 5 миллионам кельвинов, а звезда состоит из одного лишь гелия, то, конечно, никаких ядерных реакций там не будет (см. § 8), но если звезда состоит из водорода, то при такой температуре уже начнется протон-протонная реакция. С другой стороны, как мы видели в § 6, центральная температура определяется массой звезды (см. формулу (6.2)). Таким образом, если химический состав звезды дан, то для того, чтобы ее эволюция описывалась треками, приведенными на рис. 13.3, необходимо, чтобы ее масса не превышала некоторое критическое значение. Например, если звезда чисто водородная, ее масса должна быть меньше 0,08M На основании только что изложенного мы должны считать ядра планетарных туманностей объектами, у которых почти весь гелий превратился благодаря ядерным реакциям в углерод, кислород или неон. В противном случае их массы были бы меньше 0,35 солнечной, а это противоречит наблюдаемым сравнительно небольшим (0,2M
Итак, современная теория внутреннего строения звезд приводит нас к выводу, что звезды, лишенные ядерных источников энергии (какими, несомненно, являются ядра планетарных туманностей), должны эволюционировать в «нормальные» белые карлики. Остается количественно рассмотреть второй, не менее важный, вопрос: как же образуются такие звезды? Что было предшествующей стадией их эволюции? Тот факт, что ядра планетарных туманностей состоят в основном из смеси углерода, кислорода и более тяжелых элементов, сам по себе означает, что мы имеем дело с сильно проэволюционировавшими объектами. Не подлежит поэтому сомнению, что «предки» планетарных туманностей не могут принадлежать к звездам главной последовательности. Значит, они значительно от нее отошли. Но такими объектами могут быть красные гиганты либо звезды «горизонтальной ветви» диаграммы Герцшпрунга — Рессела для достаточно старых скоплений (см. § 12). В настоящую эпоху у старых скоплений «сходят» с этой диаграммы звезды с массой около 1,1M Как мы видели в предыдущем параграфе, стадия эволюции красных гигантов заканчивается «гелиевой вспышкой», когда во всем гелиевом ядре «загорается» тройная реакция превращения гелия в углерод. Расчеты показывают, что масса гелиевого ядра к этому моменту находится в пределах 0,4 Прежде всего обратим внимание на низкую наблюдаемую скорость расширения планетарных туманностей — в среднем около 30 км/с. Естественно сделать отсюда вывод, что вещество туманности «оторвалось» от звезды там, где параболическая скорость того же порядка. Отсюда, полагая массу внутренней части звезды равной 0,8M Важным аргументом в пользу образования планетарных туманностей из наружных слоев красных гигантов является обнаружение значительного избытка инфракрасного излучения практически от всех планетарных туманностей. Это излучение обусловлено находящимися в туманности пылевыми частицами, которые более или менее равномерно перемешаны с горячим газом. Физические условия в планетарных туманностях (прежде всего — высокая температура находящейся там плазмы) исключают возможность образования пылинок из газовой среды. Это означает, что пылинки, находящиеся в планетарных туманностях, имеют реликтовое происхождение, т. е. они там существуют с начала образования туманности и медленно разрушаются (например, в результате столкновений с протонами и жесткими квантами). С другой стороны, в холодных, протяженных атмосферах красных гигантов, где значительная часть газа уже находится в молекулярном состоянии, имеются все условия для образования пылинок. По-видимому, основная часть космической пыли попадает в межзвездную среду именно таким способом, т. е. путем рассеяния в ней планетарных туманностей.
В 1975 г. было обнаружено излучение в радиолинии CO (
По-видимому, с проблемой планетарных туманностей связаны обнаруженные недавно методами внеатмосферной астрономии «точечные» источники мягкого рентгеновского излучения, оказавшиеся очень горячими (температура поверхности T Таким образом, с точки зрения современной теории звездной эволюции образование планетарных туманностей и их ядер есть закономерный процесс эволюции красных гигантов. Является ли такой путь образования белых карликов единственно возможным? Можно только утверждать, что такой путь (через образование планетарных туманностей) является весьма распространенным. Вряд ли, однако, он привел к образованию всех белых карликов. Например, можно себе представить постепенное истечение вещества из наружных слоев некоторых красных гигантов, в противоположность «дискретному» отделению оболочки, приводящему к образованию планетарных туманностей. Наконец, «классический», раньше всех открытый белый карлик — знаменитый спутник Сириуса — входит в состав двойной системы. А в таких системах условия эволюции звезд весьма специфичны. Об этом будет идти речь в § 14. Глава 14 Эволюция звезд в тесных двойных системах В предыдущем параграфе довольно подробно рассматривалась эволюция звезд. Необходимо, однако, сделать важную оговорку: речь шла об эволюции одиночных, изолированных звезд. Как же будет протекать эволюция звезд, образующих двойную (или вообще кратную) систему? Не будет ли при этом одна звезда «мешать» нормальной эволюции своей соседки? Вопрос этот имеет принципиально важное значение прежде всего потому, что кратность — чрезвычайно распространенное явление в звездном мире. Приблизительно половина всех звезд главной последовательности входит в состав кратных систем. Для верхней части этой последовательности, содержащей массивные, горячие звезды спектральных классов О и В, доля звезд, входящих в кратные системы, составляет по крайней мере 70%. Заметим, что у звезд II типа населения (см. § 1) кратность — явление довольно редкое. Интерес исследователей к эволюции звезд в двойных системах, особенно тесных, стимулируется еще и тем обстоятельством, что некоторые в высшей степени любопытные звезды наблюдаются только в двойных системах. Прежде всего — это новые звезды, вспышки которых уже давно привлекают к себе самое пристальное внимание астрономов. Особый интерес представляют сейчас рентгеновские звезды, о которых речь будет идти в конце этой книги. Похоже на то, что они также всегда встречаются только в тесных двойных системах. Не менее примечателен и тот факт, что некоторые категории космических объектов явно избегают двойных систем. Значит, что-то им там «мешает». Примером таких объектов являются знаменитые пульсары, о которых будет идти речь в четвертой части этой книги. Основной характеристикой звезды, определяющей весь ее эволюционный путь, является масса. Чем больше масса, тем быстрее эволюционирует звезда, тем быстрее в ее недрах выгорает водород и она переходит в стадию красных гигантов и сверхгигантов. Однако в 1951 г. советские ученые П. П. Паренаго и А. Г. Масевич обратили внимание на то, что у тесных двойных систем компонента с большей светимостью, как правило, обладает меньшей массой. Надо заметить, что в то время теория звездной эволюции (о которой речь шла в § 12) совершенно не была разработана. Ситуация в тесных двойных системах все же представлялась странной: более массивная компонента там находится на главной последовательности, в то время как менее массивная обладает избыточной светимостью, т. е. является «почти гигантом», или «субгигантом». По мере развития теории звездной эволюции стало ясно, что субгиганты — это звезды, уже успевшие продвинуться в своей эволюции настолько, что они покинули главную последовательность. Но тогда возникает вполне закономерный вопрос: почему же звезды с заведомо меньшей массой продвинулись в своей эволюции дальше, чем более массивные звезды? Этот известный в звездной астрономии результат получил название «парадокс Алголя», по имени знаменитой затменной звездной пары, где этот парадокс явно выражен. В 1955 г. было дано вполне разумное объяснение указанному парадоксу. Звезда высокой светимости в паре обладала большей массой вначале. Однако, исчерпав существенную часть своего ядерного горючего, она стала «раздуваться». При этом довольно значительная часть ее массы «перетекла» на соседнюю компоненту, отчего масса последней стала превышать массу более быстро эволюционирующей звезды. Таким образом, важнейшим процессом, определяющим эволюцию звезд в двойной системе, является обмен массами между ними. Поэтому нельзя рассматривать эволюцию звезд в двойных системах как проходящую с постоянной массой. Как же происходит процесс обмена материей между компонентами двойной системы? Рассмотрим двойную систему, массы компонент которой M1 и M2, а орбита круговая радиуса a. Тогда из простой теории тяготения следует, что существуют для каждой из компонент такие поверхности, за пределами которых частицы вещества уже не сдерживаются гравитационным притяжением соответствующей звезды. Это объясняется действием на указанные частицы гравитационного притяжения от второй звезды, а также центробежной силы, обусловленной общим вращением системы. Если частицы находятся на самих этих поверхностях, достаточно им сообщить сколь угодно малую скорость, направленную «наружу», и они уйдут из сферы притяжения этой звезды. Если же частицы находятся в области, окружающей точку L1 (рис. 14.1), то они, покидая первую звезду, будут захвачены притяжением ее соседки. Поверхность, обладающая такими свойствами, называется «поверхностью нулевой скорости», или «критической поверхностью Роша», а точка L1, через которую вещество может перетекать из одной звезды в другую,— «внутренней лагранжевой точкой».
Поверхность Роша состоит из двух замкнутых полостей, окружающих обе звезды и имеющих общую точку L1. Радиус каждой из таких полостей может быть представлен приближенной формулой
Формула (14.1) дает вполне удовлетворительную точность для 0,3 < M1/M2 < 20. Рассмотрим теперь следующую модель эволюции звезд в тесной двойной системе. Пока обе компоненты двойной системы пребывали на главной последовательности, их радиусы были меньше радиусов соответствующих полостей Роша, определяемых формулой (14.1). Когда исчерпается значительная часть водородного горючего в центральной части быстрее эволюционирующей более массивной звезды, радиус последней станет увеличиваться, в то время как радиус второй компоненты останется неизменным. Таким образом, более массивная компонента станет «разбухать», пока ее наружная часть не заполнит свою полость Роша (см. рис. 14.1). После этого расширение главной компоненты прекратится, так как избыточная ее масса, выходящая за пределы полости Роша, начнет «переливаться» во вторую компоненту, масса которой начнет расти. Скорость потери массы эволюционирующей звездой очень быстро растет по мере роста радиуса этой звезды после достижения им величины радиуса полости Роша. Расчеты показывают, что убыль массы за единицу времени q дается формулой
где величина n зависит от структуры звезды (так называемый «политропный индекс»). Можно принять, что n = 3, и тогда для того, чтобы обмен массами между компонентами двойной системы шел в более или менее приемлемом темпе, необходимо, чтобы В первом приближении можно принять, что в процессе эволюции газ, выброшенный эволюционирующей звездой, не покинет пределы двойной системы, т. е. ее полная масса M = M1 + M2 сохраняется. При таком вполне естественном предположении расстояние между компонентами будет в процессе эволюции меняться согласно формуле
Можно убедиться, что минимальное расстояние между компонентами двойной системы будет тогда, когда в процессе «перекачки» массы от эволюционирующей компоненты к неэволюционирующей массы обеих звезд сравняются.
Как же будет происходить эволюция в такой системе? Для конкретности рассмотрим, например, случай, когда масса эволюционирующей компоненты равна пяти солнечным массам, а отношение масс компонент равно 2. Теоретическая зависимость радиуса такой звезды (если бы она была одиночной) от времени приведена на рис. 14.2. Можно видеть, что «разбухание» звезды в процессе эволюции проходит три стадии: A) Первая стадия, связанная с выгоранием водорода в центре звезды и медленным увеличением ее радиуса после того как звезда стала уходить с главной последовательности (см. рис. 12.2). B) Быстрое расширение оболочки звезды, связанное со сжатием ее ядра после того, как там выгорел водород. Эта стадия продолжается до тех пор, пока вследствие повышения температуры сжимающегося ядра включится тройная гелиевая реакция, о которой речь шла в § 8. C) Эта стадия наступает после выгорания гелия, когда ядро начнет опять сжиматься и нагреваться, пока не начнутся ядерные реакции на углероде. Описанная эволюция одиночной звезды будет нарушена тем раньше, чем ближе расположены компоненты друг к другу. Например, если в нашем случае период двойной системы около одного дня, то уже на стадии A звезда заполнит свою полость Роша и начнется обмен массой со второй компонентой. Если период порядка нескольких десятков дней, то это произойдет на стадии B. И, наконец, если период больше трех месяцев — на стадии C. Впрочем, следует заметить, что фаза C, которую достигают в одиночном состоянии далеко не все звезды, исследована очень плохо, и мы здесь этой стадией заниматься не будем. В последние годы было выполнено довольно много численных расчетов эволюции с обменом масс в двойных системах. Эти расчеты показывают, что следует различать два этапа в таком обмене масс. Вначале скорость перетекания массы от эволюционирующей компоненты ко второй очень велика; существенная часть массы теряется эволюционирующей компонентой за время, близкое к «шкале Кельвина — Гельмгольца» (см. § 3):
где величины со звездочками выражаются в солнечных единицах. Это дает для средней скорости обмена масс значение
По-видимому, в такой стадии «быстрого обмена массами» находятся двойные системы типа знаменитой системы В дальнейшем эволюция в такой системе пойдет значительно медленнее и скорость перетекания массы сильно уменьшится. Вместе с тем светимость уже ставшей менее массивной, эволюционирующей компоненты изменится мало. Длительность этой фазы эволюции образовавшегося таким образом «субгиганта» примерно такая же, как и длительность эволюции первоначально более массивной звезды, когда она «спокойно» сидела на главной последовательности. Однако по сравнению со звездой той же массы, принадлежащей к главной последовательности, которая получилась после «обмена», субгигант имеет раз в 10 большую светимость. Мы сейчас описали эволюцию двойной системы на стадии A. Стадия B протекает по-разному у более массивных и у менее массивных звезд. Разница объясняется тем, что, как мы видели в § 12, в процессе эволюции у менее массивных звезд образуется сверхплотное вырожденное ядро. Фаза быстрого обмена массой будет общей для всех звезд, если обмен начинается на стадии B. Затем, однако, наступают различия. У более массивных звезд темп дальнейшей эволюции протекает значительно быстрее. Если первоначальная масса эволюционирующей компоненты превышает три солнечные массы, то после включения в ядре тройной гелиевой реакции расширение звезды останавливается и скорость вытекания массы с ее поверхности резко замедляется и даже прекращается совсем. Такая звезда, как полагает польский астроном Б. Пачинский, много работавший в этой области, будет похожа на так называемую звезду типа Вольфа — Райе — весьма горячий объект, в спектре которого наблюдаются широкие полосы излучения. Если же масса первичной звезды сравнительно невелика, быстрое расширение ее оболочки на стадии красного гиганта останавливается по другой причине: наступает вырождение в области ядра звезды. И в этом случае скорость вытекания массы резко замедлится. Звезда будет излучать за счет водородных реакций в тонкой оболочке, окружающей ядро (см. § 12). Светимость эволюционирующей звезды будет достаточно велика: раз в 100 больше, чем светимость звезды такой же массы, находящейся на главной последовательности. Интересно отметить, что к концу этой фазы масса проэволюционировавшей компоненты сильно уменьшается: она может быть в пять и даже в 10 раз меньше массы вторичной компоненты, «вобравшей» в себя существенную часть первоначальной массы своей «соседки». «Наглотавшаяся» соседским веществом вторичная компонента все еще будет оставаться на главной последовательности, причем из-за существенно увеличившейся массы ее светимость может даже превосходить светимость проэволюционировавшей компоненты. Именно такая ситуация наблюдается в тесных двойных системах типа Алголя. На заключительном этапе, когда в эволюционирующей звезде останется совсем мало массы, ее радиус начнет уменьшаться и она, по-видимому, превращается в белый карлик. Набросанная выше картина эволюции двойных систем на стадиях A и B подтверждается огромным количеством наблюдений. В частности, эта картина непринужденно объясняет давно известный эмпирический факт, что избыточная светимость эволюционирующей компоненты тем больше, чем меньше отношение масс M1/M2. Интересные проблемы возникают при анализе дальнейшей эволюции вторичной компоненты. Дело осложняется тем, что перетекающий на вторичную компоненту газ несет с собой большой вращательный момент, обусловленный орбитальным движением, теряющей массу эволюционирующей звезды. По этой причине вокруг вторичной компоненты может образоваться быстро вращающийся газовый диск, который как бы «аккумулирует» в себе большую часть избыточного момента (рис. 14.3). В предельном случае, когда существенная часть массы эволюционирующей компоненты и ее орбитального вращательного момента перейдет ко второй компоненте и в окружающий ее быстро вращающийся газовый диск, расстояние между компонентами значительно (в 3—4 раза) уменьшится. При этом можно оценить, что свыше половины массы двойной системы и по крайней мере половина ее вращательного момента будут сосредоточены в газовом диске. Заметим, что наличие плотных газовых дисков и колец в двойных системах доказывается наблюдениями.
Выше были обрисованы основные тенденции эволюции звезд в тесных двойных системах. Впрочем, следует оговориться, что понятие «тесный» вовсе не означает «геометрическую» близость компонент. «Тесной» мы называем такую систему, у которой эволюционирующая компонента на какой-нибудь фазе заполнит свою полость Роша. Но мы уже видели, что на стадии C (см. рис. 14.1) это может произойти, когда расстояния между компонентами порядка астрономической единицы, а периоды обращения по орбитам исчисляются годами. Поэтому, с точки зрения звездной эволюции, большинство двойных систем являются «тесными». Существенно подчеркнуть, что рассматривавшаяся выше эволюция таких систем носит медленный, спокойный, отнюдь не катастрофический характер. Между тем астрономам уже давно известны классы резко нестационарных звезд, которые всегда входят в состав двойных систем и не наблюдаются как «одиночники». Это новые и новоподобные звезды, а также вспыхивающие звезды типа U Близнецов. Двойные системы, куда входят эти странные объекты, отличаются рядом любопытных особенностей. Прежде всего они, как правило, обладают очень короткими периодами — обычно порядка нескольких часов. Обе компоненты — карликовые звезды, расположенные очень близко друг от друга. Часто спектр таких объектов довольно «поздний», класса К или М, на который накладываются широкие линии излучения, а также непрерывный спектр очень горячей компоненты. Все говорит о том, что «красная» компонента такой системы (карлик!) заполняет свою полость Роша и через «внутреннюю лагранжеву точку» теряет массу, которая перетекает на горячую компоненту двойной системы. Как и в случае «спокойной» эволюции в двойной системе, вокруг этой компоненты образуется быстро вращающийся, достаточно массивный газовый диск, который излучает эмиссионные линии. «Активной» компонентой в такой системе является компактная горячая звезда, окруженная указанным диском, на которую из последнего падает поток вещества. Похоже на то, что эта компонента уже прошла свою эволюцию и когда-то передала значительную часть своего вещества соседней звезде. А теперь «соседка» в порядке «взаимной любезности» «возвращает обратно» проэволюционировавшей звезде взятое у нее много миллионов лет назад вещество. Отличительным свойством вспышек новых и новоподобных звезд является их повторяемость («рекуррентность»). Интервалы между вспышками у новоподобных звезд около 100 лет. Можно полагать, что у более интенсивно вспыхивавших новых эти интервалы исчисляются сроками порядка нескольких тысяч лет. Повторяемость вспышек новых следует хотя бы из того простого факта, что ежегодное их количество в Галактике порядка нескольких десятков. Следовательно, если бы не было повторяемости, за пару миллиардов лет в Галактике вспыхнули бы как новые все звезды — вывод явно абсурдный. Значит, существует некоторый класс звезд, которые многократно вспыхивают. Вряд ли следует сомневаться в том, что проэволюционировавшая, горячая компактная звезда представляет собой объект, сходный с белым карликом и весьма бедный водородом (см. § 12). Между тем от заполняющей свою полость Роша красной компоненты на проэволюционировавшую звезду все время падает богатый водородом газ[ 34 ]. Газ этот, после того как он накопится в поверхностном слое горячей звезды в течение сотен и тысяч лет, может стать причиной теплового взрыва, носящего как бы «локальный» характер, т. е. не охватывающего всю структуру звезды как целого. При таком взрыве выбрасывается довольно значительное количество массы, порядка 10-4—10-5 массы Солнца, как это следует из спектральных наблюдений новых звезд. Заметим, что примерно такая же масса «перетечет» на горячую компактную звезду от соседней компоненты за время между двумя вспышками. В этой чисто качественной картине вспышек новых звезд еще многое не ясно. Прежде всего — что это за ядерные реакции, «питаемые» накапливающимся в поверхностных слоях проэволюционировавшей звезды водородом? На сколько вспышек хватит «ресурсов» двойной системы? На что будет похожа такая система, когда фаза вспышки окончится? Все эти интересные вопросы пока еще только ждут ответа. Звезды типа U Близнецов характеризуются значительно большей частотой повторяемости вспышек и их меньшей амплитудой (рис. 14.4). Так же как и новые звезды в периодах между вспышками, звезды этого типа — очень компактные горячие объекты низкой светимости. Примечательно, однако, что при вспышках звезд типа U Близнецов не наблюдается никаких следов выброшенного газа. С другой стороны, в спектрах этих звезд, полученных в «спокойное» время между вспышками, так же как и у новых, наблюдаются линии излучения, указывающие на существование газового диска. Похоже, что механизм быстро чередующихся взрывов у звезд типа U Близнецов совсем не такой, как у новых. Эти звезды еще ждут своих исследователей — наблюдателей и теоретиков.
Таким образом, эволюция в тесных двойных системах может привести к рождению «сиамских близнецов», неких патологических «уродов», которые мы наблюдаем как новые звезды, звезды типа U Близнецов (сиамских?) и пр. В четвертой части этой книги будут обсуждаться еще более удивительные двойные системы. Сказанного достаточно, чтобы заключить, что двойственность звезды есть решающий фактор, определяющий ее эволюцию. Вопрос о происхождении тесных двойных систем уже давно, еще в конце прошлого века, был предметом многочисленных дискуссий. Конкурировали две гипотезы: а) совместное образование обеих компонент системы из первичного газово-пылевого облака; б) деление одной, первоначально очень быстро вращающейся звезды на две части. Вторая теория, которой некогда придерживались многие выдающиеся математики и механики (например, Пуанкаре), носила довольно формальный характер и сталкивалась со значительными теоретическими трудностями. Поэтому в последние десятилетия практически все астрономы придерживались, казалось бы, вполне естественной гипотезы об одновременном образовании обеих компонент системы. Правда, при этом возникала классическая трудность — как избавиться от слишком быстрого осевого вращения образующихся из диффузной среды звезд? Ведь звезды с массой, меньшей чем у Солнца, согласно наблюдениям, вращаются очень медленно. Предлагалось несколько довольно остроумных гипотез объясняющих это обстоятельство, но ощущение некоторой неопределенности оставалось. Однако в самое последнее время, точнее, осенью 1982 г. на этом, казалось бы, совершенно «спокойном участке фронта» произошли бурные события. Группа голландских астрономов с помощью скромного телескопа с диаметром зеркала 0,9 м на Европейской обсерватории в Чили провела тщательное фотометрическое исследование звезд, входящих в состав известного скопления Плеяд. Из нескольких сотен звезд, находящихся в этом скоплении, изучались сравнительно яркие объекты поздних спектральных классов G и ранних К. Массы таких звезд лишь немного меньше солнечной (1—0,8 M Что же является причиной такого неравномерного распределения яркости по дискам звезд? Первое, что приходит в голову,— искать причину в больших пятнах (вроде солнечных, но побольше), покрывающих поверхности звезд. Однако, как это видно на примере Солнца, пятна возникают более или менее случайно, поэтому строго периодической картины вариаций блеска звезд они не дадут. Между тем кривые блеска звезд в Плеядах остаются неизменными за 1500 звездных оборотов! Кроме того, амплитуда вариаций блеска не связана с величиной звездного магнитного поля, что можно было ожидать, если бы причиной наблюдаемой переменности были бы солнечные пятна. И наконец, было обнаружено, что температура поверхности звезды меняется примерно на 100 К за цикл, между тем как наличие темных пятен привело бы только к эффективному уменьшению излучающей поверхности без изменения ее температуры. Эти звезды вращаются приблизительно в 100 раз быстрее «нормальных» звезд того же самого спектрального класса. Всего удивительнее, что в тех же Плеядах слегка более массивные звезды вращаются «нормально», т. е. значительно более медленно. Создается впечатление, что звезды рождаются и первое время живут в состоянии очень быстрого вращения, а затем на каком-то этапе эволюции быстро теряют свой вращательный момент, который переходит в орбитальный. Из-за быстрого вращения эти звезды имеют форму сильно сплюснутых трехосных эллипсоидов, и даже, возможно, грушевидных фигур равновесия, привлекавших внимание некоторых теоретиков много десятилетий тому назад. Эти исследования находятся, конечно, в самой ранней стадии. Очень важно провести аналогичные наблюдения для других скоплений и ассоциаций, в частности, для ассоциации в Орионе. Возраст этой ассоциации примерно в 10 раз меньше, чем Плеяд. Поэтому можно ожидать, что в стадии деления там будут звезды несколько более массивные (и, следовательно, более ранних спектральных классов), чем в Плеядах. И, конечно, возникает интригующая возможность по-новому подойти к проблеме образования Солнечной системы. Примечания:1 1 На этих диаграммах вместо спектральных классов по оси абсцисс приведены показатели цвета B - V . Значению B - V , равному -0,4 -0,2, соответствуют звезды классов О и В, значению B -V , равному +1,6, звезды класса М. 2 2 Звезды, имеющие «сферическое» пространственное распределение, обладают значительными хаотическими скоростями (до 100 км/с), в то время как у «плоских» объектов эти скорости малы ( 10 км/с). Такие различия в хаотических скоростях тесно связаны с различием в пространственном распределении (аналогия с известной барометрической формулой: более горячий газ образует более протяженную атмосферу). 3 3 Зависимость была установлена для цефеид, находящихся в Магеллановых Облаках — ближайших к нам галактиках. Так как расстояния до всех обнаруженных там цефеид практически одинаковы, то их видимые величины непосредственно определяют светимости, поскольку расстояние до Магеллановых Облаков известно. 16 Точнее, разница в давлении газа на разной глубине внутри звезды. 17 Заметим, однако, что при фокусировке мощного лазерного луча на мишень (которая, конечно, при этом мгновенно испарится) в течение 10-9 секунды может возникнуть давление отдачи на нее (обусловленное испаряющимися атомами), достигающее 1012 атмосфер! 18 Именно по этой причине поток реликтового излучения Вселенной (как это ни парадоксально) почти равен нулю. «Почти» потому, что могут быть незначительные отклонения от строгой изотропии. 19 Так как излучение выходит наружу из слоев звездной атмосферы с несколько разной глубиной, температуры которых немного отличаются, Te имеет смысл «эффективной температуры». 20 Коэффициент поглощения вещества определяется следующим образом. Пусть мы имеем некоторый слой вещества с очень малой толщиной l и плотностью . После прохождения этого слоя интенсивность излучения уменьшится на величину Il. При этом предполагается, что сам слой не излучает. 21 Существует еще специфический механизм поглощения излучения полностью ионизованным газом («свободно-свободные переходы»), но у звезд, сходных с Солнцем, этот механизм несуществен. 22 Заметим, что при такой ситуации водород «выгорает» только внутри конвективной зоны, между тем как наружные слои звезды, где сосредоточена основная часть ее массы, не перемешиваются с конвективным ядром. 23 В отдельных редких случаях при катастрофических процессах, являющихся причиной взрыва звезд, реакции с нейтронами, по-видимому, могут иметь существенное значение. 24 Символ [ ] здесь означает концентрацию данного сорта частиц 25 В последние годы В. А. Любимов и его коллеги экспериментально нашли, что масса покоя нейтрино конечна и близка к 20 эВ. Этот результат (значение которого трудно было бы переоценить, особенно для космологии) нуждается в независимом подтверждении. 26 Любопытно отметить, что предыдущее межледниковое время, бывшее на Земле около 100 000 лет назад, закончилось очень быстро, по геологическим масштабам даже внезапно. За какую-нибудь сотню лет теплолюбивые виды животных покинули воды Гренландии и Ньюфаундленда. Имеются некоторые основания полагать, что наше межледниковое время подходит к концу, по-видимому, столь же быстро. 27 На это обстоятельство впервые указал советский физик-теоретик Я. И. Френкель в 1928 г. За два года до этого английский физик Р. Фаулер впервые применил теорию вырожденного газа для объяснения природы белых карликов. Полная теория белых карликов была развита Чандрасекаром. 28 Учет «нейтронизации» вещества при большой плотности (см. § 22) снижает этот предел до 1,2M. 29 Из-за наличия сильного магнитного поля излучение белых карликов должно быть слегка поляризовано по кругу. Изучая зависимость этой поляризации от времени, можно, в принципе, определить периоды вращения белых карликов. В тех немногих случаях, для которых эти очень деликатные наблюдения были выполнены, периоды осевого вращения оказались довольно значительными, порядка суток. Этот результат должен иметь существенное значение для проблемы звездной эволюции. 30 Некоторая часть красных гигантов у молодых звездных скоплений может быть протозвездами, находящимися в стадии сжатия и движущимися к главной последовательности. Однако, в принципе, их можно отличить от «настоящих» красных гигантов, являющихся более или менее «старыми» звездами (см. § 5). 31 Мысль о том, что красные гиганты образуются из звезд главной последовательности после выгорания ядерного горючего в недрах последних, впервые была высказана Э. Эпиком еще в 1938 г. 32 Следует, однако, иметь в виду, что содержание тяжелых элементов у разных шаровых скоплений меняется в довольно широких пределах. Более того, даже у одного скопления разные звезды иногда имеют разные Z. Действительность всегда богаче любой схемы. 33 Планетарные туманности в этих ближайших к нам галактиках удалены от нас на практически одинаковое расстояние, поэтому их светимости сравнительно легко определяются из видимых звездных величин. 34 Тщательные поляриметрические наблюдения доказали, что бывшая новая, вспыхнувшая в созвездии Геркулеса в 1934 г., вращается вокруг оси с периодом 142 секунды, причем скорость вращения постепенно растет. Такое быстрое вращение легко объясняется потоком газа от второй компоненты (красного карлика), приносящего большой вращательный момент. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Главная | Контакты | Нашёл ошибку | Прислать материал | Добавить в избранное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 1033 г, на его объем, равный
1033 г, на его объем, равный  1,4
1,4  1033 см3, легко найти среднюю плотность (или удельный вес) солнечного вещества, которая будет около 1,4 г/см3, т. е. больше плотности воды. Ясно, что в центральных областях Солнца плотность должна быть значительно выше средней. У большинства карликовых звезд средняя плотность превосходит солнечную. Естественно возникает вопрос: как согласовать наше утверждение, что недра Солнца и звезд находятся в газообразном состоянии со столь высокими плотностями вещества? Ответ на этот вопрос состоит в том, что температура звездных недр, как мы скоро убедимся, очень высока (значительно выше, чем в поверхностных слоях), что исключает возможность существования там твердой или жидкой фазы вещества.
1033 см3, легко найти среднюю плотность (или удельный вес) солнечного вещества, которая будет около 1,4 г/см3, т. е. больше плотности воды. Ясно, что в центральных областях Солнца плотность должна быть значительно выше средней. У большинства карликовых звезд средняя плотность превосходит солнечную. Естественно возникает вопрос: как согласовать наше утверждение, что недра Солнца и звезд находятся в газообразном состоянии со столь высокими плотностями вещества? Ответ на этот вопрос состоит в том, что температура звездных недр, как мы скоро убедимся, очень высока (значительно выше, чем в поверхностных слоях), что исключает возможность существования там твердой или жидкой фазы вещества.  1011/106 = 106 секунд
1011/106 = 106 секунд  10 суток!
10 суток!  , где G — гравитационная постоянная (см. стр. 15), M — масса, лежащая внутри сферы радиуса R. По мере падения к центру как M, так и R будут меняться, следовательно, будет меняться и g. Мы, однако, не сделаем большой ошибки в нашей оценке, если предположим, что M и R остаются постоянными. Применив к решению нашей задачи элементарную формулу механики, связывающую пройденный при свободном падении путь R с величиной ускорения g, получим уже выведенную в § 3 первой части формулу (3.6)
, где G — гравитационная постоянная (см. стр. 15), M — масса, лежащая внутри сферы радиуса R. По мере падения к центру как M, так и R будут меняться, следовательно, будет меняться и g. Мы, однако, не сделаем большой ошибки в нашей оценке, если предположим, что M и R остаются постоянными. Применив к решению нашей задачи элементарную формулу механики, связывающую пройденный при свободном падении путь R с величиной ускорения g, получим уже выведенную в § 3 первой части формулу (3.6)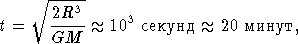
 R
R , a M
, a M  M
M . Таким образом, если бы никакая сила не противодействовала гравитации, наружные слои звезды буквально рухнули бы, а звезда катастрофически бы сжалась за какую-нибудь долю часа!
. Таким образом, если бы никакая сила не противодействовала гравитации, наружные слои звезды буквально рухнули бы, а звезда катастрофически бы сжалась за какую-нибудь долю часа!  R, где
R, где  — средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/2. Тогда условие гидростатического равновесия запишется так:
— средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/2. Тогда условие гидростатического равновесия запишется так:
 и температуры T. Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P =
и температуры T. Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P = 
 T. С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
T. С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.  . Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1/2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
. Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1/2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
 /
/ c может быть порядка 1/10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа, т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
c может быть порядка 1/10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа, т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.  =
=  kT будет около 10-9 эрг или
kT будет около 10-9 эрг или  1000 эВ.
1000 эВ.  , равнялась бы 1/2. Если бы там был только полностью ионизованный гелий, то
, равнялась бы 1/2. Если бы там был только полностью ионизованный гелий, то  = 4/3 (так как при ионизации одного атома гелия с атомной массой 4 образуются три частицы — ядро гелия плюс два электрона). Наконец, если бы вещество недр звезды состояло только из тяжелых элементов (кислорода, углерода, железа и пр.), то средняя молекулярная масса его при полной ионизации всех атомов была бы близка к 2, так как для таких элементов атомная масса приблизительно вдвое больше, чем число электронов в атоме.
= 4/3 (так как при ионизации одного атома гелия с атомной массой 4 образуются три частицы — ядро гелия плюс два электрона). Наконец, если бы вещество недр звезды состояло только из тяжелых элементов (кислорода, углерода, железа и пр.), то средняя молекулярная масса его при полной ионизации всех атомов была бы близка к 2, так как для таких элементов атомная масса приблизительно вдвое больше, чем число электронов в атоме.  0,3 означает, что на каждые 10 атомов водорода приходится приблизительно один атом гелия. Относительное количество тяжелых элементов весьма мало. Например, атомов кислорода примерно в тысячу раз меньше, чем водорода. Тем не менее роль тяжелых элементов в структуре внутренних областей звезд довольно значительна, так как они сильно влияют на непрозрачность звездного вещества. Среднюю молекулярную массу звезды мы можем теперь определить простой формулой:
0,3 означает, что на каждые 10 атомов водорода приходится приблизительно один атом гелия. Относительное количество тяжелых элементов весьма мало. Например, атомов кислорода примерно в тысячу раз меньше, чем водорода. Тем не менее роль тяжелых элементов в структуре внутренних областей звезд довольно значительна, так как они сильно влияют на непрозрачность звездного вещества. Среднюю молекулярную массу звезды мы можем теперь определить простой формулой:
 незначительна. Решающее значение для величины средней молекулярной массы имеют X и Y . Для звезд центральной части главной последовательности (в частности, для Солнца)
незначительна. Решающее значение для величины средней молекулярной массы имеют X и Y . Для звезд центральной части главной последовательности (в частности, для Солнца)  = 0,6. Так как величина
= 0,6. Так как величина  для большинства звезд меняется в очень незначительных пределах, мы можем написать простую формулу для центральных температур различных звезд, выразив их массы и радиусы в долях солнечной массы M
для большинства звезд меняется в очень незначительных пределах, мы можем написать простую формулу для центральных температур различных звезд, выразив их массы и радиусы в долях солнечной массы M и солнечного радиуса R
и солнечного радиуса R :
:
 — температура центральных областей Солнца. Выше, мы грубо оценили T
— температура центральных областей Солнца. Выше, мы грубо оценили T в 10 миллионов кельвинов. Точные вычисления дают значение T
в 10 миллионов кельвинов. Точные вычисления дают значение T = 14 миллионов кельвинов. Из формулы (6.4) следует, например, что температура недр массивных горячих (на поверхности!) звезд спектрального класса В раза в 2—3 выше температуры солнечных недр, в то время как у красных карликов центральные температуры раза в 2—3 ниже солнечных.
= 14 миллионов кельвинов. Из формулы (6.4) следует, например, что температура недр массивных горячих (на поверхности!) звезд спектрального класса В раза в 2—3 выше температуры солнечных недр, в то время как у красных карликов центральные температуры раза в 2—3 ниже солнечных.  107 К характерна не только для самых центральных областей звезд, но и для окружающего центр звезды большого объема. Учитывая, что плотность звездного вещества растет по направлению к центру, мы можем сделать вывод, что основная часть массы звезды имеет температуру, во всяком случае превышающую
107 К характерна не только для самых центральных областей звезд, но и для окружающего центр звезды большого объема. Учитывая, что плотность звездного вещества растет по направлению к центру, мы можем сделать вывод, что основная часть массы звезды имеет температуру, во всяком случае превышающую  5 миллионов кельвинов. Если мы еще вспомним, что большая часть массы Вселенной заключена в звездах, то напрашивается вывод, что вещество Вселенной, как правило, горячее и плотное. Следует, однако, к этому добавить, что речь идет о современной Вселенной: в далеком прошлом и будущем состояние вещества Вселенной было и будет совсем другим. Об этом речь шла во введении к этой книге.
5 миллионов кельвинов. Если мы еще вспомним, что большая часть массы Вселенной заключена в звездах, то напрашивается вывод, что вещество Вселенной, как правило, горячее и плотное. Следует, однако, к этому добавить, что речь идет о современной Вселенной: в далеком прошлом и будущем состояние вещества Вселенной было и будет совсем другим. Об этом речь шла во введении к этой книге. в единичном интервале частот равна
в единичном интервале частот равна

 . Последняя определяется как количество энергии, протекающее через площадку в один квадратный сантиметр в единичном интервале частот за одну секунду внутри телесного угла в один стерадиан в некотором заданном направлении, причем площадка перпендикулярна к этому направлению. Если для всех направлений величина интенсивности одинакова, то она связана с плотностью излучения простым соотношением
. Последняя определяется как количество энергии, протекающее через площадку в один квадратный сантиметр в единичном интервале частот за одну секунду внутри телесного угла в один стерадиан в некотором заданном направлении, причем площадка перпендикулярна к этому направлению. Если для всех направлений величина интенсивности одинакова, то она связана с плотностью излучения простым соотношением


 с
с  стер, а количество излучения, протекающее в каком-нибудь одном направлении («вверх» или «вниз»), будет несколько больше: F =
стер, а количество излучения, протекающее в каком-нибудь одном направлении («вверх» или «вниз»), будет несколько больше: F =  I = 3
I = 3  1023 эрг/см2
1023 эрг/см2  с. Между тем величина потока излучения Солнца в его центральной части,. где-нибудь на расстоянии
с. Между тем величина потока излучения Солнца в его центральной части,. где-нибудь на расстоянии  100 000 км от его центра (это в семь раз меньше солнечного радиуса), будет равна H = L/4
100 000 км от его центра (это в семь раз меньше солнечного радиуса), будет равна H = L/4 r2 = 4
r2 = 4  1033/1021 = 4
1033/1021 = 4  1012 эрг/см2
1012 эрг/см2  с, т.е. в тысячу миллиардов раз меньше. Это объясняется тем, что в солнечных недрах поток излучения наружу («вверх») почти в точности равен потоку внутрь («вниз»). Все дело в этом «почти». Ничтожная разница в интенсивности поля излучения и определяет всю картину излучения звезды. Именно по этой причине мы сделали выше оговорку, что поле излучения почти равновесно. При строго равновесном поле излучения никакого потока излучения не должно быть! Еще раз подчеркнем, что отклонения реального поля излучения в недрах звезд от планковского совершенно ничтожны, что видно из малости отношения H/F
с, т.е. в тысячу миллиардов раз меньше. Это объясняется тем, что в солнечных недрах поток излучения наружу («вверх») почти в точности равен потоку внутрь («вниз»). Все дело в этом «почти». Ничтожная разница в интенсивности поля излучения и определяет всю картину излучения звезды. Именно по этой причине мы сделали выше оговорку, что поле излучения почти равновесно. При строго равновесном поле излучения никакого потока излучения не должно быть! Еще раз подчеркнем, что отклонения реального поля излучения в недрах звезд от планковского совершенно ничтожны, что видно из малости отношения H/F  10-12.
10-12.  107 К максимум энергии в планковском спектре приходится на рентгеновский диапазон. Это следует из хорошо известного из элементарной теории излучения закона Вина:
107 К максимум энергии в планковском спектре приходится на рентгеновский диапазон. Это следует из хорошо известного из элементарной теории излучения закона Вина:
 m — длина волны, на которую приходится максимум функции Планка. При T = 107 К
m — длина волны, на которую приходится максимум функции Планка. При T = 107 К  m = 3
m = 3  10-8 см или 3A — типичный рентгеновский диапазон. Количество лучистой энергии, заключенной в недрах Солнца (или какой-нибудь другой звезды), сильно зависит от распределения температуры с глубиной, так как u
10-8 см или 3A — типичный рентгеновский диапазон. Количество лучистой энергии, заключенной в недрах Солнца (или какой-нибудь другой звезды), сильно зависит от распределения температуры с глубиной, так как u  T4. Точная теория звездных недр позволяет получить такую зависимость, откуда следует, что у нашего светила запас лучистой энергии около 1045 эрг. Если бы ничто не сдерживало кванты этого жесткого излучения, они за пару секунд покинули бы Солнце и эта чудовищная вспышка, несомненно, сожгла бы все живое на поверхности Земли. Это не происходит потому, что излучение буквально «заперто» внутри Солнца. Огромная толща вещества Солнца служит надежным «буфером». Кванты излучения, непрерывно и очень часто поглощаясь атомами, ионами и электронами плазмы солнечного вещества, лишь чрезвычайно медленно «просачиваются» наружу. В процессе такой «диффузии» они существенно меняют свое основное качество — энергию. Если в недрах звезд, как мы видели, их энергия соответствует рентгеновскому диапазону, то с поверхности звезды кванты выходят уже сильно «отощавшими» — их энергия уже соответствует преимущественно оптическому диапазону.
T4. Точная теория звездных недр позволяет получить такую зависимость, откуда следует, что у нашего светила запас лучистой энергии около 1045 эрг. Если бы ничто не сдерживало кванты этого жесткого излучения, они за пару секунд покинули бы Солнце и эта чудовищная вспышка, несомненно, сожгла бы все живое на поверхности Земли. Это не происходит потому, что излучение буквально «заперто» внутри Солнца. Огромная толща вещества Солнца служит надежным «буфером». Кванты излучения, непрерывно и очень часто поглощаясь атомами, ионами и электронами плазмы солнечного вещества, лишь чрезвычайно медленно «просачиваются» наружу. В процессе такой «диффузии» они существенно меняют свое основное качество — энергию. Если в недрах звезд, как мы видели, их энергия соответствует рентгеновскому диапазону, то с поверхности звезды кванты выходят уже сильно «отощавшими» — их энергия уже соответствует преимущественно оптическому диапазону.  1057 частиц — протонов и электронов. При температуре T
1057 частиц — протонов и электронов. При температуре T  107 К средняя энергия, приходящаяся на одну частицу, будет равна
107 К средняя энергия, приходящаяся на одну частицу, будет равна  kT = 2
kT = 2  10-9 эрг, откуда следует, что запас тепловой энергии Солнца WT составляет весьма солидную величину
10-9 эрг, откуда следует, что запас тепловой энергии Солнца WT составляет весьма солидную величину  4
4  1048 эрг. При наблюдаемой мощности солнечного излучения L
1048 эрг. При наблюдаемой мощности солнечного излучения L = 4
= 4  1033 эрг/с этого запаса хватает на 1015 секунд или
1033 эрг/с этого запаса хватает на 1015 секунд или  30 миллионов лет. Вопрос состоит в том, почему Солнце имеет именно ту светимость, которую мы наблюдаем? Или, другими словами, почему находящийся в состоянии гидростатического равновесия газовый шар с массой, равной массе Солнца, имеет совершенно определенный радиус и совершенно определенную температуру поверхности, с которой излучение выходит наружу? Ибо светимость любой звезды, в том числе и Солнца, можно представить простым выражением
30 миллионов лет. Вопрос состоит в том, почему Солнце имеет именно ту светимость, которую мы наблюдаем? Или, другими словами, почему находящийся в состоянии гидростатического равновесия газовый шар с массой, равной массе Солнца, имеет совершенно определенный радиус и совершенно определенную температуру поверхности, с которой излучение выходит наружу? Ибо светимость любой звезды, в том числе и Солнца, можно представить простым выражением


 1052 эрг превышает сумму гравитационной и тепловой энергии Солнца более чем в 1000 раз. То же самое относится и к подавляющему большинству других звезд. Этого запаса хватит для поддержания излучения Солнца на сто миллиардов лет! Конечно, отсюда не следует, то Солнце будет излучать в течение столь огромного промежутка времени на современном уровне. Но во всяком случае ясно, что запасов ядерного горючего у Солнца и звезд более чем достаточно.
1052 эрг превышает сумму гравитационной и тепловой энергии Солнца более чем в 1000 раз. То же самое относится и к подавляющему большинству других звезд. Этого запаса хватит для поддержания излучения Солнца на сто миллиардов лет! Конечно, отсюда не следует, то Солнце будет излучать в течение столь огромного промежутка времени на современном уровне. Но во всяком случае ясно, что запасов ядерного горючего у Солнца и звезд более чем достаточно.  107 К средняя энергия тепловых движений частиц близка к 1000 эВ. Эта энергия слишком мала для того, чтобы, преодолев кулоновские силы отталкивания при столкновении двух ядер, попасть в другое ядро и тем самым вызвать ядерное превращение. Необходимая энергия должна быть по крайней мере в десятки раз больше. Существенно, однако, что при максвелловом распределении скоростей всегда найдутся частицы, энергия которых будет значительно превышать среднюю. Их, правда, будет мало, но только они, сталкиваясь с другими ядрами, вызывают ядерные превращения и, следовательно, выделение энергии. Количество таких аномально быстрых, но все же «тепловых» ядер весьма чувствительным образом зависит от температуры вещества. Казалось бы, при такой ситуации ядерные реакции, сопровождающиеся выделением энергии, могут быстро повысить температуру вещества, отчего в свою очередь их скорость резко увеличивается, и звезда смогла бы за сравнительно короткое время израсходовать свой запас ядерного горючего путем увеличения своей светимости. Ведь энергия не может накапливаться в звезде — это привело бы к резкому увеличению давления газа и звезда просто взорвалась бы как перегретый паровой котел. Поэтому вся выделившаяся в недрах звезд ядерная энергия должна покидать звезду; этот процесс и определяет светимость звезды. Но в том-то и дело, что какие бы ни были термоядерные реакции, они не могут идти в звезде с произвольной скоростью. Как только, хотя бы в незначительной степени, произойдет локальный (т. е. местный) разогрев вещества звезды, последнее из-за возросшего давления расширится, отчего согласно формуле Клапейрона произойдет охлаждение. При этом скорость ядерных реакций сразу же упадет и вещество, таким образом, вернется к своему первоначальному состоянию. Этот процесс восстановления нарушенного вследствие локального разогрева гидростатического равновесия, как мы видели раньше, идет весьма быстро.
107 К средняя энергия тепловых движений частиц близка к 1000 эВ. Эта энергия слишком мала для того, чтобы, преодолев кулоновские силы отталкивания при столкновении двух ядер, попасть в другое ядро и тем самым вызвать ядерное превращение. Необходимая энергия должна быть по крайней мере в десятки раз больше. Существенно, однако, что при максвелловом распределении скоростей всегда найдутся частицы, энергия которых будет значительно превышать среднюю. Их, правда, будет мало, но только они, сталкиваясь с другими ядрами, вызывают ядерные превращения и, следовательно, выделение энергии. Количество таких аномально быстрых, но все же «тепловых» ядер весьма чувствительным образом зависит от температуры вещества. Казалось бы, при такой ситуации ядерные реакции, сопровождающиеся выделением энергии, могут быстро повысить температуру вещества, отчего в свою очередь их скорость резко увеличивается, и звезда смогла бы за сравнительно короткое время израсходовать свой запас ядерного горючего путем увеличения своей светимости. Ведь энергия не может накапливаться в звезде — это привело бы к резкому увеличению давления газа и звезда просто взорвалась бы как перегретый паровой котел. Поэтому вся выделившаяся в недрах звезд ядерная энергия должна покидать звезду; этот процесс и определяет светимость звезды. Но в том-то и дело, что какие бы ни были термоядерные реакции, они не могут идти в звезде с произвольной скоростью. Как только, хотя бы в незначительной степени, произойдет локальный (т. е. местный) разогрев вещества звезды, последнее из-за возросшего давления расширится, отчего согласно формуле Клапейрона произойдет охлаждение. При этом скорость ядерных реакций сразу же упадет и вещество, таким образом, вернется к своему первоначальному состоянию. Этот процесс восстановления нарушенного вследствие локального разогрева гидростатического равновесия, как мы видели раньше, идет весьма быстро. 
 , где
, где  — коэффициент поглощения, рассчитанный на единицу массы
— коэффициент поглощения, рассчитанный на единицу массы
 близка к одному миллиметру. Даже странно на первый взгляд, что газ может быть настолько непрозрачным. Ведь мы, находясь в земной атмосфере, видим предметы, удаленные на десятки километров! Такая огромная непрозрачность газообразного вещества звездных недр объясняется его высокой плотностью, а главное — высокой температурой, которая делает газ ионизованным. Ясно, что разница в температуре на протяжении одного миллиметра должна быть совершенно ничтожной. Ее можно грубо оценить, считая перепад температуры от центра Солнца к его поверхности равномерным. Тогда получается, что разность температур на расстоянии 1 мм близка к одной стотысячной градуса. Соответственно этому, ничтожной будет и разница между интенсивностью излучения, идущего «сверху» и «снизу». Следовательно, поток излучения будет ничтожно мал по сравнению с интенсивностью, о чем речь уже шла выше.
близка к одному миллиметру. Даже странно на первый взгляд, что газ может быть настолько непрозрачным. Ведь мы, находясь в земной атмосфере, видим предметы, удаленные на десятки километров! Такая огромная непрозрачность газообразного вещества звездных недр объясняется его высокой плотностью, а главное — высокой температурой, которая делает газ ионизованным. Ясно, что разница в температуре на протяжении одного миллиметра должна быть совершенно ничтожной. Ее можно грубо оценить, считая перепад температуры от центра Солнца к его поверхности равномерным. Тогда получается, что разность температур на расстоянии 1 мм близка к одной стотысячной градуса. Соответственно этому, ничтожной будет и разница между интенсивностью излучения, идущего «сверху» и «снизу». Следовательно, поток излучения будет ничтожно мал по сравнению с интенсивностью, о чем речь уже шла выше.  интенсивность излучения «сверху» будет равна интенсивности излучения «снизу», так как температуры строго равны.
интенсивность излучения «сверху» будет равна интенсивности излучения «снизу», так как температуры строго равны. 
 означает изменение температуры при продвижении на один сантиметр от центра звезды. Если бы температура была строго постоянной, то
означает изменение температуры при продвижении на один сантиметр от центра звезды. Если бы температура была строго постоянной, то  было бы равно нулю. Формула (7.10) выражает то, о чем уже шла речь выше. Поток излучения от звезды (а следовательно, ее светимость) тем больше, чем меньше непрозрачность звездного вещества и сильнее перепад температуры в звездных недрах.
было бы равно нулю. Формула (7.10) выражает то, о чем уже шла речь выше. Поток излучения от звезды (а следовательно, ее светимость) тем больше, чем меньше непрозрачность звездного вещества и сильнее перепад температуры в звездных недрах.  = 3M/4
= 3M/4 R3.
R3. 

 , будем иметь
, будем иметь 
 , для большинства звезд меняется в незначительных пределах. Непрозрачность звездного вещества
, для большинства звезд меняется в незначительных пределах. Непрозрачность звездного вещества  зависит в первую очередь от наличия в нем тяжелых элементов. Дело в том, что водород и гелий в условиях звездных недр полностью ионизованы и в таком состоянии поглощать излучение почти не могут. Ведь для того, чтобы квант излучения был поглощен, необходимо, чтобы его энергия была полностью израсходована на отрыв электрона от ядра, т. е. на ионизацию. Если же атомы водорода и гелия полностью ионизованы, то, выражаясь просто, и отрывать нечего
зависит в первую очередь от наличия в нем тяжелых элементов. Дело в том, что водород и гелий в условиях звездных недр полностью ионизованы и в таком состоянии поглощать излучение почти не могут. Ведь для того, чтобы квант излучения был поглощен, необходимо, чтобы его энергия была полностью израсходована на отрыв электрона от ядра, т. е. на ионизацию. Если же атомы водорода и гелия полностью ионизованы, то, выражаясь просто, и отрывать нечего
 не очень сильно меняющейся от звезды к звезде. Точные расчеты показывают, что для горячих массивных звезд
не очень сильно меняющейся от звезды к звезде. Точные расчеты показывают, что для горячих массивных звезд 
 1, между тем как для красных карликов значение
1, между тем как для красных карликов значение  раз в 10 больше. Таким образом, из формулы (7.11) следует, что светимость «нормальной» (т. е. находящейся в равновесии на главной последовательности) звезды в первую очередь зависит от ее массы. Если подставить численное значение всех входящих в формулу коэффициентов, то ее можно переписать в виде
раз в 10 больше. Таким образом, из формулы (7.11) следует, что светимость «нормальной» (т. е. находящейся в равновесии на главной последовательности) звезды в первую очередь зависит от ее массы. Если подставить численное значение всех входящих в формулу коэффициентов, то ее можно переписать в виде

 20, а средняя молекулярная масса
20, а средняя молекулярная масса  = 0,6 (см. выше). Тогда L/L
= 0,6 (см. выше). Тогда L/L = 5,6. Нас не должно смущать то обстоятельство, что L/L
= 5,6. Нас не должно смущать то обстоятельство, что L/L не получилось равным единице. Это объясняется чрезвычайной грубостью нашей модели. Точные расчеты, учитывающие распределение температуры Солнца с глубиной, дают значение L/L
не получилось равным единице. Это объясняется чрезвычайной грубостью нашей модели. Точные расчеты, учитывающие распределение температуры Солнца с глубиной, дают значение L/L близкое к единице.
близкое к единице. 

 и P обозначают плотность и давление. После того как объем переместился вверх (или, другими словами, «претерпел возмущение»), причем его внутреннее давление уравновешено давлением окружающей среды, плотность его должна отличаться от плотности указанной среды. Это объясняется тем, что в процессе подъема и расширения нашего объема его плотность менялась по особому, так называемому «адиабатическому» закону. В этом случае будем иметь
и P обозначают плотность и давление. После того как объем переместился вверх (или, другими словами, «претерпел возмущение»), причем его внутреннее давление уравновешено давлением окружающей среды, плотность его должна отличаться от плотности указанной среды. Это объясняется тем, что в процессе подъема и расширения нашего объема его плотность менялась по особому, так называемому «адиабатическому» закону. В этом случае будем иметь
 = cp/c3 — отношение удельных теплоемкостей при постоянном давлении и постоянном объеме. Для идеального газа, из которого состоит вещество «нормальных» звезд, cp/c3 = 5/3. А теперь посмотрим, что у нас получилось. После перемещения объема вверх действующее на него давление окружающей среды по-прежнему равно внутреннему, между тем гравитационная сила, действующая на единицу объема, стала другой, так как изменилась плотность. Теперь ясно, что если эта плотность окажется больше плотности окружающей среды, объем начнет опускаться вниз, пока не займет своего первоначального положения. Если же эта плотность в процессе адиабатического расширения стала меньше плотности окружающей среды, объем будет продолжать свое движение вверх, «всплывая» под действием силы Архимеда. В первом случае состояние среды будет устойчивым. Это означает, что любое, случайно возникшее движение газа в среде будет как бы «подавляться» и элемент вещества, который начал было перемещаться, сразу же вернется на свое прежнее место. Во втором же случае состояние среды будет неустойчивым. Малейшее возмущение (от которого никогда нельзя «застраховаться») будет все больше и больше усиливаться. В среде возникнут беспорядочные движения газа «вверх» и «вниз». Движущиеся массы газа будут переносить с собой содержащуюся в них тепловую энергию. Наступит состояние конвекции. Конвекция очень часто наблюдается в земных условиях (вспомним, например, как греется вода в чайнике, поставленном на плиту). Перенос энергии путем конвекции качественно отличается от обсуждавшегося в предыдущем параграфе переноса энергии путем лучеиспускания. В последнем случае, как мы видели, количество переносимой в потоке излучения энергии ограничено непрозрачностью звездного вещества. Например, если непрозрачность очень велика, то при данном перепаде температуры количество переносимой энергии будет сколь угодно мало. Не так обстоит дело с переносом энергии путем конвекции. Из самой сущности этого механизма следует, что количество переносимой конвекцией энергии никакими свойствами среды не ограничено.
= cp/c3 — отношение удельных теплоемкостей при постоянном давлении и постоянном объеме. Для идеального газа, из которого состоит вещество «нормальных» звезд, cp/c3 = 5/3. А теперь посмотрим, что у нас получилось. После перемещения объема вверх действующее на него давление окружающей среды по-прежнему равно внутреннему, между тем гравитационная сила, действующая на единицу объема, стала другой, так как изменилась плотность. Теперь ясно, что если эта плотность окажется больше плотности окружающей среды, объем начнет опускаться вниз, пока не займет своего первоначального положения. Если же эта плотность в процессе адиабатического расширения стала меньше плотности окружающей среды, объем будет продолжать свое движение вверх, «всплывая» под действием силы Архимеда. В первом случае состояние среды будет устойчивым. Это означает, что любое, случайно возникшее движение газа в среде будет как бы «подавляться» и элемент вещества, который начал было перемещаться, сразу же вернется на свое прежнее место. Во втором же случае состояние среды будет неустойчивым. Малейшее возмущение (от которого никогда нельзя «застраховаться») будет все больше и больше усиливаться. В среде возникнут беспорядочные движения газа «вверх» и «вниз». Движущиеся массы газа будут переносить с собой содержащуюся в них тепловую энергию. Наступит состояние конвекции. Конвекция очень часто наблюдается в земных условиях (вспомним, например, как греется вода в чайнике, поставленном на плиту). Перенос энергии путем конвекции качественно отличается от обсуждавшегося в предыдущем параграфе переноса энергии путем лучеиспускания. В последнем случае, как мы видели, количество переносимой в потоке излучения энергии ограничено непрозрачностью звездного вещества. Например, если непрозрачность очень велика, то при данном перепаде температуры количество переносимой энергии будет сколь угодно мало. Не так обстоит дело с переносом энергии путем конвекции. Из самой сущности этого механизма следует, что количество переносимой конвекцией энергии никакими свойствами среды не ограничено. 
 107 К уже не имеют практически никакой возможности проникнуть друг в друга. Только при значительно более высоких температурах, которые в некоторых случаях реализуются внутри звезд, возможны ядерные реакции на тяжелых элементах.
107 К уже не имеют практически никакой возможности проникнуть друг в друга. Только при значительно более высоких температурах, которые в некоторых случаях реализуются внутри звезд, возможны ядерные реакции на тяжелых элементах.  -частицы), причем избыточная масса выделяется в виде энергии, нагревающей среду, в которой происходят реакции. В звездных недрах существуют два пути превращения водорода в гелий, отличающиеся разной последовательностью ядерных реакций. Первый путь обычно называется «протон-протонная реакция», второй — «углеродно-азотная реакция».
-частицы), причем избыточная масса выделяется в виде энергии, нагревающей среду, в которой происходят реакции. В звездных недрах существуют два пути превращения водорода в гелий, отличающиеся разной последовательностью ядерных реакций. Первый путь обычно называется «протон-протонная реакция», второй — «углеродно-азотная реакция». 
 означает нейтрино, а
означает нейтрино, а  — гамма-квант.
— гамма-квант.  10-5 эрг.
10-5 эрг.  8Be + e+ +
8Be + e+ +  . Заметим, что нейтрино, образовавшиеся при этой реакции, как раз и обнаружили при помощи уникальной дорогостоящей установки. Об этом важном эксперименте подробно будет рассказано в следующем параграфе. Радиоактивный бериллий 8Ве весьма неустойчив и быстро распадается на две альфа-частицы. Наконец, последняя, третья ветвь протон-протонной реакции включает в себя следующие звенья: 7Ве после захвата электрона превращается в 7Li, который, захватив протон, превращается в неустойчивый изотоп 8Ве, распадающийся, как и во второй цепи, на две альфа-частицы.
. Заметим, что нейтрино, образовавшиеся при этой реакции, как раз и обнаружили при помощи уникальной дорогостоящей установки. Об этом важном эксперименте подробно будет рассказано в следующем параграфе. Радиоактивный бериллий 8Ве весьма неустойчив и быстро распадается на две альфа-частицы. Наконец, последняя, третья ветвь протон-протонной реакции включает в себя следующие звенья: 7Ве после захвата электрона превращается в 7Li, который, захватив протон, превращается в неустойчивый изотоп 8Ве, распадающийся, как и во второй цепи, на две альфа-частицы. 
 -квант. Изотоп 13N, претерпевая
-квант. Изотоп 13N, претерпевая  -распад с испусканием позитрона и нейтрино, превращается в изотоп углерода 13С. Последний, сталкиваясь с протоном, превращается в обычное ядро азота 14N. При этой реакции также испускается
-распад с испусканием позитрона и нейтрино, превращается в изотоп углерода 13С. Последний, сталкиваясь с протоном, превращается в обычное ядро азота 14N. При этой реакции также испускается  -квант. Далее, ядро азота сталкивается с протоном, после чего образуется радиоактивный изотоп кислорода 15O и
-квант. Далее, ядро азота сталкивается с протоном, после чего образуется радиоактивный изотоп кислорода 15O и  -квант. Затем этот изотоп путем
-квант. Затем этот изотоп путем  -распада превращается в изотоп азота 15N. Наконец, последний, присоединив к себе во время столкновения протон, распадается на обычный углерод и гелий. Вся цепь реакций представляет собой последовательное «утяжеление» ядра углерода путем присоединения протонов с последующими
-распада превращается в изотоп азота 15N. Наконец, последний, присоединив к себе во время столкновения протон, распадается на обычный углерод и гелий. Вся цепь реакций представляет собой последовательное «утяжеление» ядра углерода путем присоединения протонов с последующими  -распадами. Последним звеном этой цепи является восстановление первоначального ядра углерода и образование нового ядра гелия за счет четырех протонов, которые в разное время один за другим присоединились к 12С и образующимся из него изотопам. Как видно, никакого изменения числа ядер 12С в веществе, в котором протекает эта реакция, не происходит. Углерод служит здесь «катализатором» реакции.
-распадами. Последним звеном этой цепи является восстановление первоначального ядра углерода и образование нового ядра гелия за счет четырех протонов, которые в разное время один за другим присоединились к 12С и образующимся из него изотопам. Как видно, никакого изменения числа ядер 12С в веществе, в котором протекает эта реакция, не происходит. Углерод служит здесь «катализатором» реакции.  -процессов это просто период полураспада. Значительно труднее определить скорость реакции, когда происходит утяжеление ядра путем присоединения протона. В этом случае надо знать вероятности проникновения протона через кулоновский барьер, а также вероятности соответствующих ядерных взаимодействий, так как само по себе проникновение протона в ядро еще не обеспечивает интересующего нас ядерного превращения. Вероятности ядерных реакций получаются из лабораторных экспериментов либо вычисляются теоретически. Для их надежного определения потребовались годы напряженной работы физиков-ядерщиков, как теоретиков, так и экспериментаторов. Числа в третьем столбце дают «время жизни» различных ядер для центральных областей звезды с температурой в 13 миллионов кельвинов и плотностью водорода 100 г/см3. Например, для того чтобы при таких условиях ядро 12С, захватив протон, превратилось в радиоактивный изотоп углерода, надо «подождать» 13 миллионов лет! Следовательно, для каждого «активного» (т. е. участвующего в цикле) ядра реакции протекают чрезвычайно медленно, но все дело в том, что ядер достаточно много.
-процессов это просто период полураспада. Значительно труднее определить скорость реакции, когда происходит утяжеление ядра путем присоединения протона. В этом случае надо знать вероятности проникновения протона через кулоновский барьер, а также вероятности соответствующих ядерных взаимодействий, так как само по себе проникновение протона в ядро еще не обеспечивает интересующего нас ядерного превращения. Вероятности ядерных реакций получаются из лабораторных экспериментов либо вычисляются теоретически. Для их надежного определения потребовались годы напряженной работы физиков-ядерщиков, как теоретиков, так и экспериментаторов. Числа в третьем столбце дают «время жизни» различных ядер для центральных областей звезды с температурой в 13 миллионов кельвинов и плотностью водорода 100 г/см3. Например, для того чтобы при таких условиях ядро 12С, захватив протон, превратилось в радиоактивный изотоп углерода, надо «подождать» 13 миллионов лет! Следовательно, для каждого «активного» (т. е. участвующего в цикле) ядра реакции протекают чрезвычайно медленно, но все дело в том, что ядер достаточно много. 



 = 89,
= 89,  = 270.
= 270. 
 106 К
106 К 
 10-2, т.е. почти в сто раз больше. Следовательно, образующийся в недрах сравнительно холодных карликовых звезд изотоп 3He весьма обилен.
10-2, т.е. почти в сто раз больше. Следовательно, образующийся в недрах сравнительно холодных карликовых звезд изотоп 3He весьма обилен.  3He + 4He; 7Li + 1H
3He + 4He; 7Li + 1H  24He; 10B + 21H
24He; 10B + 21H  34He и некоторые другие. Так как заряд ядра — «мишени», с которой сталкивается протон, невелик, кулоновское отталкивание не так значительно, как в случае столкновений с ядрами углерода и азота. Поэтому скорость этих реакций сравнительно велика. Уже при температуре около миллиона кельвинов они идут достаточно быстро. Однако, в отличие от ядер углерода и азота, ядра легких элементов не восстанавливаются в процессе дальнейших реакций, а необратимо расходуются. Именно поэтому обилие легких элементов на Солнце и в звездах так ничтожно мало. Они уже давно «выгорели» на самых ранних стадиях существования звезд. Когда температура внутри сжимающейся под действием силы тяжести протозвезды достигнет
34He и некоторые другие. Так как заряд ядра — «мишени», с которой сталкивается протон, невелик, кулоновское отталкивание не так значительно, как в случае столкновений с ядрами углерода и азота. Поэтому скорость этих реакций сравнительно велика. Уже при температуре около миллиона кельвинов они идут достаточно быстро. Однако, в отличие от ядер углерода и азота, ядра легких элементов не восстанавливаются в процессе дальнейших реакций, а необратимо расходуются. Именно поэтому обилие легких элементов на Солнце и в звездах так ничтожно мало. Они уже давно «выгорели» на самых ранних стадиях существования звезд. Когда температура внутри сжимающейся под действием силы тяжести протозвезды достигнет  1 миллиона кельвинов, первые ядерные реакции, которые там будут протекать,— это реакции на легких ядрах. Тот факт, что в атмосфере Солнца и звезд наблюдаются слабые спектральные линии лития и бериллия, требует объяснения. Он может указывать на отсутствие перемешивания между самыми наружными слоями Солнца и «глубинными» слоями, где температура уже превышает 2 миллиона кельвинов — значение, при котором эти элементы «выгорели» бы. Следует, однако, иметь в виду и совершенно другую возможность. Дело в том, что, как сейчас доказано, в активных областях Солнца (там, где происходят вспышки) заряженные частицы ускоряются до весьма высоких энергий. Такие частицы, сталкиваясь с ядрами атомов, образующих солнечную атмосферу, могут давать (и дают!) различные ядерные реакции. Свыше 10 лет назад при помощи гамма-детектора, установленного на запущенном в США специализированном спутнике «OSO-7» («Седьмая орбитальная солнечная лаборатория»), были обнаружены во время яркой вспышки на Солнце 4 августа 1972 г. две спектральные линии в этом диапазоне. Одна линия, имеющая энергию квантов 0,511 МэВ, отождествляется с излучением, возникающим при аннигиляции электронов с позитронами, другая с энергией 2,22 МэВ излучается при образовании дейтерия из протонов и нейтронов. Эти важные эксперименты как раз и демонстрируют, что в активных областях Солнца и, конечно, звезд идут ядерные реакции. Только такими реакциями можно объяснить аномально высокое обилие лития в атмосферах некоторых звезд и наличие линий технеция у звезд редкого спектрального класса S. Ведь самый долгоживущий изотоп технеция имеет период полураспада около 200 000 лет. Именно по этой причине его нет на Земле. Только ядерные реакции в поверхностных слоях звезд могут объяснить наличие линий технеция в спектрах упомянутых выше звезд.
1 миллиона кельвинов, первые ядерные реакции, которые там будут протекать,— это реакции на легких ядрах. Тот факт, что в атмосфере Солнца и звезд наблюдаются слабые спектральные линии лития и бериллия, требует объяснения. Он может указывать на отсутствие перемешивания между самыми наружными слоями Солнца и «глубинными» слоями, где температура уже превышает 2 миллиона кельвинов — значение, при котором эти элементы «выгорели» бы. Следует, однако, иметь в виду и совершенно другую возможность. Дело в том, что, как сейчас доказано, в активных областях Солнца (там, где происходят вспышки) заряженные частицы ускоряются до весьма высоких энергий. Такие частицы, сталкиваясь с ядрами атомов, образующих солнечную атмосферу, могут давать (и дают!) различные ядерные реакции. Свыше 10 лет назад при помощи гамма-детектора, установленного на запущенном в США специализированном спутнике «OSO-7» («Седьмая орбитальная солнечная лаборатория»), были обнаружены во время яркой вспышки на Солнце 4 августа 1972 г. две спектральные линии в этом диапазоне. Одна линия, имеющая энергию квантов 0,511 МэВ, отождествляется с излучением, возникающим при аннигиляции электронов с позитронами, другая с энергией 2,22 МэВ излучается при образовании дейтерия из протонов и нейтронов. Эти важные эксперименты как раз и демонстрируют, что в активных областях Солнца и, конечно, звезд идут ядерные реакции. Только такими реакциями можно объяснить аномально высокое обилие лития в атмосферах некоторых звезд и наличие линий технеция у звезд редкого спектрального класса S. Ведь самый долгоживущий изотоп технеция имеет период полураспада около 200 000 лет. Именно по этой причине его нет на Земле. Только ядерные реакции в поверхностных слоях звезд могут объяснить наличие линий технеция в спектрах упомянутых выше звезд.  12C +
12C +  , ведущая к образованию устойчивого изотопа углерода с выделением значительного количества энергии. При каждой такой реакции выделяется 7,3 миллиона электронвольт.
, ведущая к образованию устойчивого изотопа углерода с выделением значительного количества энергии. При каждой такой реакции выделяется 7,3 миллиона электронвольт.  -частиц приходится всего лишь один изотоп 8Ве), все же скорость «тройной» реакции оказывается достаточной для выделения в недрах очень горячих звезд значительного количества энергии. Зависимость энерговыделения от температуры исключительно велика. Например, для температур порядка 100—200 миллионов кельвинов
-частиц приходится всего лишь один изотоп 8Ве), все же скорость «тройной» реакции оказывается достаточной для выделения в недрах очень горячих звезд значительного количества энергии. Зависимость энерговыделения от температуры исключительно велика. Например, для температур порядка 100—200 миллионов кельвинов

 -распада, выдвинул смелую гипотезу о существовании новой элементарной частицы. Эта частица, получившая название «нейтрино», должна иметь весьма удивительные свойства. Будучи электрически нейтральной, она должна обладать массой покоя ничтожно малой, скорее всего, даже нулевой. По этим причинам нейтрино должны обладать совершенно исключительной способностью проникать через огромные толщи вещества. Подсчитано, что без заметного поглощения пучок нейтрино с энергией в миллион электронвольт может пройти через стальную плиту, толщина которой в сотню раз превосходит расстояние от Земли до ближайших звезд! Ясно, что для таких частиц пройти «насквозь» через любую звезду, как говорится, «пустое дело»... Но столь удивительно слабая способность нейтрино взаимодействовать с веществом имеет и свою «обратную сторону». Потребовалось 25 лет после гениального теоретического предсказания Паули, чтобы эта необычайная частица была обнаружена в лабораторном эксперименте и тем самым из разряда гипотетических перешла в разряд вполне реальных элементарных частиц.
-распада, выдвинул смелую гипотезу о существовании новой элементарной частицы. Эта частица, получившая название «нейтрино», должна иметь весьма удивительные свойства. Будучи электрически нейтральной, она должна обладать массой покоя ничтожно малой, скорее всего, даже нулевой. По этим причинам нейтрино должны обладать совершенно исключительной способностью проникать через огромные толщи вещества. Подсчитано, что без заметного поглощения пучок нейтрино с энергией в миллион электронвольт может пройти через стальную плиту, толщина которой в сотню раз превосходит расстояние от Земли до ближайших звезд! Ясно, что для таких частиц пройти «насквозь» через любую звезду, как говорится, «пустое дело»... Но столь удивительно слабая способность нейтрино взаимодействовать с веществом имеет и свою «обратную сторону». Потребовалось 25 лет после гениального теоретического предсказания Паули, чтобы эта необычайная частица была обнаружена в лабораторном эксперименте и тем самым из разряда гипотетических перешла в разряд вполне реальных элементарных частиц.  /25 МэВ = 1039 с-1, а поток их на Земле N/4
/25 МэВ = 1039 с-1, а поток их на Земле N/4 r2 = 1011 см-2
r2 = 1011 см-2  с-1. Это огромная величина. Мы буквально «купаемся» в потоке солнечных нейтрино.
с-1. Это огромная величина. Мы буквально «купаемся» в потоке солнечных нейтрино. 

 10-36 (заметим, что величина 10-36 получила специальное название «s. n. u.» — «единица солнечных нейтрино»). Между тем, если бы принятая в настоящее время модель солнечных недр была точной, эта величина должна была бы быть в три раза больше.
10-36 (заметим, что величина 10-36 получила специальное название «s. n. u.» — «единица солнечных нейтрино»). Между тем, если бы принятая в настоящее время модель солнечных недр была точной, эта величина должна была бы быть в три раза больше.  14 МэВ). Заметим, что количество таких нейтрино составляет ничтожную долю от полного нейтринного потока, который почти не зависит от модели Солнца.
14 МэВ). Заметим, что количество таких нейтрино составляет ничтожную долю от полного нейтринного потока, который почти не зависит от модели Солнца.  5 миллиардов лет, которые существует Солнце. Расчеты показывают, что максимальная концентрация изотопа 3He достигается на расстоянии 0,6 солнечного радиуса. Представим себе теперь, что по какой-либо причине произошло внезапное перемешивание солнечных недр. Оно должно повлечь за собой значительное увеличение концентрации 3He в области центра Солнца, так как туда поступит материал, где концентрация 3He выше. Так как концентрация этого изотопа определяет скорость протон-протонной реакции, энерговыделение резко возрастает, и мы получим ситуацию, обсуждавшуюся выше.
5 миллиардов лет, которые существует Солнце. Расчеты показывают, что максимальная концентрация изотопа 3He достигается на расстоянии 0,6 солнечного радиуса. Представим себе теперь, что по какой-либо причине произошло внезапное перемешивание солнечных недр. Оно должно повлечь за собой значительное увеличение концентрации 3He в области центра Солнца, так как туда поступит материал, где концентрация 3He выше. Так как концентрация этого изотопа определяет скорость протон-протонной реакции, энерговыделение резко возрастает, и мы получим ситуацию, обсуждавшуюся выше. 

 )1/4, где L1 — «нормальная» светимость, L
)1/4, где L1 — «нормальная» светимость, L — современная. Отсюда вытекает, что в настоящее время температура нашей планеты должна быть градусов на 30 ниже, чем в «нормальные» периоды, когда мощность солнечного излучения близка к L1. Следует, правда, заметить, что наличие на Земле мощного облачного слоя и атмосферной циркуляции должно значительно сгладить разницу средних температур Земли в «нормальное» и в наше время. По-видимому, с учетом этого обстоятельства разница должна быть равна 10—15 К. А это означает, что сейчас Земля переживает ледниковый период!
— современная. Отсюда вытекает, что в настоящее время температура нашей планеты должна быть градусов на 30 ниже, чем в «нормальные» периоды, когда мощность солнечного излучения близка к L1. Следует, правда, заметить, что наличие на Земле мощного облачного слоя и атмосферной циркуляции должно значительно сгладить разницу средних температур Земли в «нормальное» и в наше время. По-видимому, с учетом этого обстоятельства разница должна быть равна 10—15 К. А это означает, что сейчас Земля переживает ледниковый период!  20 г/см3. Тот факт, что средняя плотность вещества в белых карликах может быть в десятки тысяч раз больше, означает, что ядра там находятся друг от друга на расстояниях, значительно меньших, чем 10-8 см. Отсюда следует, что электронные оболочки атомов как бы «раздавлены» и ядра отделены от электронов. В этом смысле мы можем говорить о веществе недр белых карликов как об очень плотной плазме. Но плазма — это прежде всего газ, т. е. такое состояние вещества, когда расстояние между образующими его частицами значительно превышает размеры последних. В нашем случае расстояние между ядрами не меньше чем
20 г/см3. Тот факт, что средняя плотность вещества в белых карликах может быть в десятки тысяч раз больше, означает, что ядра там находятся друг от друга на расстояниях, значительно меньших, чем 10-8 см. Отсюда следует, что электронные оболочки атомов как бы «раздавлены» и ядра отделены от электронов. В этом смысле мы можем говорить о веществе недр белых карликов как об очень плотной плазме. Но плазма — это прежде всего газ, т. е. такое состояние вещества, когда расстояние между образующими его частицами значительно превышает размеры последних. В нашем случае расстояние между ядрами не меньше чем  10-10 см, в то время как размеры ядер ничтожно малы — порядка 10-12 см.
10-10 см, в то время как размеры ядер ничтожно малы — порядка 10-12 см. 
 106, а плотность
106, а плотность  выражена, как обычно, в граммах на кубический сантиметр. Формула (10.1) заменяет для вырожденного газа уравнение Клапейрона и является его «уравнением состояния». Характерной особенностью этого уравнения является то, что температура в него не входит. Кроме того, в отличие от уравнения Клапейрона, где давление пропорционально первой степени плотности, здесь зависимость давления от плотности более сильная. Это нетрудно понять. Ведь давление пропорционально концентрации частиц и их скорости. Концентрация частиц, естественно, пропорциональна плотности, а скорость частиц вырожденного газа растет с ростом плотности, так как при этом, согласно принципу Паули, растет количество «избыточных» частиц, вынужденных двигаться с большими скоростями.
выражена, как обычно, в граммах на кубический сантиметр. Формула (10.1) заменяет для вырожденного газа уравнение Клапейрона и является его «уравнением состояния». Характерной особенностью этого уравнения является то, что температура в него не входит. Кроме того, в отличие от уравнения Клапейрона, где давление пропорционально первой степени плотности, здесь зависимость давления от плотности более сильная. Это нетрудно понять. Ведь давление пропорционально концентрации частиц и их скорости. Концентрация частиц, естественно, пропорциональна плотности, а скорость частиц вырожденного газа растет с ростом плотности, так как при этом, согласно принципу Паули, растет количество «избыточных» частиц, вынужденных двигаться с большими скоростями.  по формуле (10.1), больше, чем по формуле (6.2), значит, газ вырожден. Отсюда получается «условие вырождения»
по формуле (10.1), больше, чем по формуле (6.2), значит, газ вырожден. Отсюда получается «условие вырождения»

 — средняя молекулярная масса. Чему же равно
— средняя молекулярная масса. Чему же равно  в недрах белых карликов? Прежде всего водорода там практически не должно быть: при таких огромных плотностях и достаточно высоких температурах он давно уже «сгорел» при ядерных реакциях. Основным элементом в недрах белых карликов должен быть гелий. Так как его атомная масса равна 4 и он при ионизации дает два электрона (при этом надо учитывать еще, что частицами, производящими давление, там являются только электроны), то средняя молекулярная масса должна быть очень близка к 2. Численно условие вырождения (10.2) записывается так:
в недрах белых карликов? Прежде всего водорода там практически не должно быть: при таких огромных плотностях и достаточно высоких температурах он давно уже «сгорел» при ядерных реакциях. Основным элементом в недрах белых карликов должен быть гелий. Так как его атомная масса равна 4 и он при ионизации дает два электрона (при этом надо учитывать еще, что частицами, производящими давление, там являются только электроны), то средняя молекулярная масса должна быть очень близка к 2. Численно условие вырождения (10.2) записывается так:
 > 2,5
> 2,5  10-4 г/см3. Это очень низкая плотность, из которой сразу же следует, что электроны в металлах должны быть вырождены (на самом деле в этом случае постоянные K и
10-4 г/см3. Это очень низкая плотность, из которой сразу же следует, что электроны в металлах должны быть вырождены (на самом деле в этом случае постоянные K и  имеют другое значение, но суть дела при этом не меняется). Если температура T близка к температуре звездных недр, т. е. около 10 миллионов кельвинов, то
имеют другое значение, но суть дела при этом не меняется). Если температура T близка к температуре звездных недр, т. е. около 10 миллионов кельвинов, то  > 1000 г/см3. Отсюда сразу же следуют два вывода:
> 1000 г/см3. Отсюда сразу же следуют два вывода:


 M/R3. Тогда при релятивистском вырождении P
M/R3. Тогда при релятивистском вырождении P  M4/3/R4, а сила, противодействующая гравитации и равная перепаду давления,
M4/3/R4, а сила, противодействующая гравитации и равная перепаду давления,
 GM/R2
GM/R2  M2/R5. Мы видим, что обе силы — гравитация и перепад давления — зависят от размеров звезды одинаковым образом: как R-5, и по-разному зависят от массы. Следовательно, должно существовать некоторое, совершенно определенное значение массы звезды, при котором обе силы уравновешиваются. Если же масса превышает некоторое критическое значение, то сила гравитации всегда будет преобладать над силой, обусловленной перепадом давления, и звезда катастрофически сожмется.
M2/R5. Мы видим, что обе силы — гравитация и перепад давления — зависят от размеров звезды одинаковым образом: как R-5, и по-разному зависят от массы. Следовательно, должно существовать некоторое, совершенно определенное значение массы звезды, при котором обе силы уравновешиваются. Если же масса превышает некоторое критическое значение, то сила гравитации всегда будет преобладать над силой, обусловленной перепадом давления, и звезда катастрофически сожмется. 
 5/3 следует, что P/R
5/3 следует, что P/R  M5/3/R6, т. е. зависимость силы, противодействующей гравитации, от R будет более сильной. Поэтому при некотором значении радиуса расширение звезды прекратится.
M5/3/R6, т. е. зависимость силы, противодействующей гравитации, от R будет более сильной. Поэтому при некотором значении радиуса расширение звезды прекратится. 






 105 г/см3. Это означает, что электронный газ в ядре вырожден (см. § 10). Следовательно, по своим свойствам вещество изотермического ядра красного гиганта не отличается от вещества белых карликов. Они сходны не только по средней плотности, но и по химическому составу и отсутствию ядерных реакций. Поэтому мы имеем все основания утверждать, что в центре красного гиганта находится ... белый карлик! Этот результат имеет большое значение для проблемы происхождения белых карликов, о чем речь будет идти в следующем параграфе.
105 г/см3. Это означает, что электронный газ в ядре вырожден (см. § 10). Следовательно, по своим свойствам вещество изотермического ядра красного гиганта не отличается от вещества белых карликов. Они сходны не только по средней плотности, но и по химическому составу и отсутствию ядерных реакций. Поэтому мы имеем все основания утверждать, что в центре красного гиганта находится ... белый карлик! Этот результат имеет большое значение для проблемы происхождения белых карликов, о чем речь будет идти в следующем параграфе. 
 — количество энергии, выделяющейся при ядерном превращении одного грамма вещества, символ
— количество энергии, выделяющейся при ядерном превращении одного грамма вещества, символ  означает изменение величины X за одну секунду. Мы можем определить возраст звезды как промежуток времени, прошедший с того момента, когда она «села» на главную последовательность, т. е. в ее недрах начались ядерные водородные реакции. Если для разных членов эволюционной последовательности известны величина светимости и среднее содержание водорода X, то не представляет труда из уравнения (12.1) найти возраст какой-нибудь определенной модели звезды на ее эволюционной последовательности. Тот, кто знает основы высшей математики, поймет, что из уравнения (12.1), являющегося простым дифференциальным уравнением, возраст звезды
означает изменение величины X за одну секунду. Мы можем определить возраст звезды как промежуток времени, прошедший с того момента, когда она «села» на главную последовательность, т. е. в ее недрах начались ядерные водородные реакции. Если для разных членов эволюционной последовательности известны величина светимости и среднее содержание водорода X, то не представляет труда из уравнения (12.1) найти возраст какой-нибудь определенной модели звезды на ее эволюционной последовательности. Тот, кто знает основы высшей математики, поймет, что из уравнения (12.1), являющегося простым дифференциальным уравнением, возраст звезды  определяется как интеграл
определяется как интеграл

 12, мы, очевидно, получим интервал времени
12, мы, очевидно, получим интервал времени  , прошедший от начала эволюции звезды. Именно это обстоятельство и выражает формула (12.2).
, прошедший от начала эволюции звезды. Именно это обстоятельство и выражает формула (12.2). 
 1,1
1,1  1,5M
1,5M . Заметим, что эволюцию звезд, масса которых меньше массы Солнца, вообще нецелесообразно рассматривать, так как время пребывания их в пределах главной последовательности превышает возраст Галактики. Это обстоятельство делает проблему эволюции звезд с малой массой «неинтересной» или, лучше сказать, «не актуальной». Заметим только, что звезды с малой массой (меньше чем
. Заметим, что эволюцию звезд, масса которых меньше массы Солнца, вообще нецелесообразно рассматривать, так как время пребывания их в пределах главной последовательности превышает возраст Галактики. Это обстоятельство делает проблему эволюции звезд с малой массой «неинтересной» или, лучше сказать, «не актуальной». Заметим только, что звезды с малой массой (меньше чем  0,3 солнечной) остаются полностью «конвективными» даже тогда, когда они находятся на главной последовательности. «Лучистое» ядро у них так никогда и не образуется. Эта тенденция хорошо видна в случае эволюции протозвезд (см. § 5). Если масса последних сравнительно велика, лучистое ядро образуется еще до того, как протозвезда «сядет» на главную последовательность. А маломассивные объекты как на протозвездной, так и на звездной стадии остаются полностью конвективными. У таких звезд температура в центре недостаточно велика для того, чтобы протон-протонный цикл полностью работал. Он обрывается на образовании изотопа 3Не, а «нормальный» 4Не уже не синтезируется. За 10 миллиардов лет (что близко к возрасту старейших звезд этого типа) в 3Не превратится около 1% водорода. Следовательно, можно ожидать, что обилие 3Не по отношению к 1Н будет аномально велико — около 3%. К сожалению, пока нет возможности проверить это предсказание теории наблюдениями. Звезды с такой малой массой — это красные карлики, температура поверхности которых совершенно недостаточна для возбуждения линий гелия в оптической области. В принципе, однако, в далекой ультрафиолетовой части спектра резонансные линии поглощения могли бы наблюдаться методами ракетной астрономии. Однако чрезвычайная слабость непрерывного спектра исключает даже эту проблематичную возможность. Следует, однако, заметить, что существенная, если не большая часть красных карликов представляет собой вспыхивающие звезды типа UV Кита (см. § 1). Сам феномен быстро повторяющихся вспышек у таких карликовых холодных звезд несомненно связан с конвекцией, которой охвачен весь их объем. Во время вспышек наблюдаются линии излучения. Может быть, удастся наблюдать и линии 3Не у таких звезд? Если масса протозвезды меньше чем 0,08M
0,3 солнечной) остаются полностью «конвективными» даже тогда, когда они находятся на главной последовательности. «Лучистое» ядро у них так никогда и не образуется. Эта тенденция хорошо видна в случае эволюции протозвезд (см. § 5). Если масса последних сравнительно велика, лучистое ядро образуется еще до того, как протозвезда «сядет» на главную последовательность. А маломассивные объекты как на протозвездной, так и на звездной стадии остаются полностью конвективными. У таких звезд температура в центре недостаточно велика для того, чтобы протон-протонный цикл полностью работал. Он обрывается на образовании изотопа 3Не, а «нормальный» 4Не уже не синтезируется. За 10 миллиардов лет (что близко к возрасту старейших звезд этого типа) в 3Не превратится около 1% водорода. Следовательно, можно ожидать, что обилие 3Не по отношению к 1Н будет аномально велико — около 3%. К сожалению, пока нет возможности проверить это предсказание теории наблюдениями. Звезды с такой малой массой — это красные карлики, температура поверхности которых совершенно недостаточна для возбуждения линий гелия в оптической области. В принципе, однако, в далекой ультрафиолетовой части спектра резонансные линии поглощения могли бы наблюдаться методами ракетной астрономии. Однако чрезвычайная слабость непрерывного спектра исключает даже эту проблематичную возможность. Следует, однако, заметить, что существенная, если не большая часть красных карликов представляет собой вспыхивающие звезды типа UV Кита (см. § 1). Сам феномен быстро повторяющихся вспышек у таких карликовых холодных звезд несомненно связан с конвекцией, которой охвачен весь их объем. Во время вспышек наблюдаются линии излучения. Может быть, удастся наблюдать и линии 3Не у таких звезд? Если масса протозвезды меньше чем 0,08M , то температура в ее недрах настолько мала, что никакие термоядерные реакции уже не могут остановить сжатие на стадии главной последовательности. Такие звезды будут непрерывно сжиматься, пока не станут белыми карликами (точнее, вырожденными красными карликами). Вернемся, однако, к эволюции более массивных звезд.
, то температура в ее недрах настолько мала, что никакие термоядерные реакции уже не могут остановить сжатие на стадии главной последовательности. Такие звезды будут непрерывно сжиматься, пока не станут белыми карликами (точнее, вырожденными красными карликами). Вернемся, однако, к эволюции более массивных звезд.  согласно наиболее детальным расчетам, выполненным с помощью ЭВМ. На этом треке цифрами отмечены характерные этапы эволюции звезды. В пояснениях к рисунку указаны сроки прохождения каждого этапа эволюции. Укажем здесь только, что участку эволюционного трека 1—2 соответствует главная последовательность, участку 6—7 — стадия красного гиганта. Интересно уменьшение светимости на участке 5—6, связанное с затратой энергии на «разбухание» звезды. На рис. 12.3 аналогичные теоретически рассчитанные треки приведены для звезд разной массы. Цифры, отмечающие различные фазы эволюции, имеют тот же смысл, что и на рис. 12.2.
согласно наиболее детальным расчетам, выполненным с помощью ЭВМ. На этом треке цифрами отмечены характерные этапы эволюции звезды. В пояснениях к рисунку указаны сроки прохождения каждого этапа эволюции. Укажем здесь только, что участку эволюционного трека 1—2 соответствует главная последовательность, участку 6—7 — стадия красного гиганта. Интересно уменьшение светимости на участке 5—6, связанное с затратой энергии на «разбухание» звезды. На рис. 12.3 аналогичные теоретически рассчитанные треки приведены для звезд разной массы. Цифры, отмечающие различные фазы эволюции, имеют тот же смысл, что и на рис. 12.2. 
 , (1—2) — горение водорода в конвективном ядре, 6,44
, (1—2) — горение водорода в конвективном ядре, 6,44  107 лет; (2—3) — общее сжатие звезды, 2,2
107 лет; (2—3) — общее сжатие звезды, 2,2  106 лет; (3—4) — возгорание водорода в слоистом источнике, 1,4
106 лет; (3—4) — возгорание водорода в слоистом источнике, 1,4  105 лет; (4—5) — горение водорода в толстом слое, 1,2
105 лет; (4—5) — горение водорода в толстом слое, 1,2  106 лет; (5—6) — расширение конвективной оболочки, 8
106 лет; (5—6) — расширение конвективной оболочки, 8  105 лет; (6—7) — фаза красного гиганта, 5
105 лет; (6—7) — фаза красного гиганта, 5  105 лет; (7—8) — возгорание гелия в ядре, 6
105 лет; (7—8) — возгорание гелия в ядре, 6  106 лет; (8—9) — исчезновение конвективной оболочки, 106 лет; (9—10) — горение гелия в ядре, 9
106 лет; (8—9) — исчезновение конвективной оболочки, 106 лет; (9—10) — горение гелия в ядре, 9  106 лет; (10—11) — вторичное расширение конвективной оболочки, 106 лет; (11—12) — сжатие ядра по мере выгорания гелия; (12—13—14) — слоистый гелиевый источник; (14—?) — нейтринные потери, красный сверхгигант.
106 лет; (10—11) — вторичное расширение конвективной оболочки, 106 лет; (11—12) — сжатие ядра по мере выгорания гелия; (12—13—14) — слоистый гелиевый источник; (14—?) — нейтринные потери, красный сверхгигант.



 с разным содержанием тяжелых элементов, 1 — главная последовательность, 2 — звездное население II типа, 3 — население I типа.
с разным содержанием тяжелых элементов, 1 — главная последовательность, 2 — звездное население II типа, 3 — население I типа.






 .
. , если гелиевая — 0,35M
, если гелиевая — 0,35M , углеродная — меньше 1,04M
, углеродная — меньше 1,04M . Соответствующие центральные температуры равны 4
. Соответствующие центральные температуры равны 4  106, 1,2
106, 1,2  108 и 6
108 и 6  108 К.
108 К.  ) массам планетарных туманностей. Ибо масса красного гиганта, из которого образовались ядро и сама планетарная туманность, должна быть немного больше солнечной. Кроме того, согласно наблюдениям (правда, довольно скудным), большая часть масс белых карликов лежит в пределах 0,5—1,0 солнечной массы. Скорее всего ядра планетарных туманностей покрыты тонкой «коркой» не успевшего «сгореть» гелия, и возможно, водорода. Учет этого обстоятельства в теоретических расчетах делает температуры ядер не такими высокими.
) массам планетарных туманностей. Ибо масса красного гиганта, из которого образовались ядро и сама планетарная туманность, должна быть немного больше солнечной. Кроме того, согласно наблюдениям (правда, довольно скудным), большая часть масс белых карликов лежит в пределах 0,5—1,0 солнечной массы. Скорее всего ядра планетарных туманностей покрыты тонкой «коркой» не успевшего «сгореть» гелия, и возможно, водорода. Учет этого обстоятельства в теоретических расчетах делает температуры ядер не такими высокими. 
 (для звезд I типа населения, у которых тяжелых элементов сравнительно много) и 0,85M
(для звезд I типа населения, у которых тяжелых элементов сравнительно много) и 0,85M (для бедных тяжелыми элементами звезд II поколения (шаровые скопления)). Для молодых скоплений звезд I типа эти массы больше, но, как правило, не превышают 1,5 солнечной. Мы можем, таким образом, сделать вывод, что массы «предков» планетарных туманностей, принадлежащих преимущественно к I типу звездного населения (диск), должны быть заключены в пределах 1,1—1,5 солнечной. При такой массе у них должны образовываться вырожденные ядра.
(для бедных тяжелыми элементами звезд II поколения (шаровые скопления)). Для молодых скоплений звезд I типа эти массы больше, но, как правило, не превышают 1,5 солнечной. Мы можем, таким образом, сделать вывод, что массы «предков» планетарных туманностей, принадлежащих преимущественно к I типу звездного населения (диск), должны быть заключены в пределах 1,1—1,5 солнечной. При такой массе у них должны образовываться вырожденные ядра.  0,5M
0,5M и почти не зависит от полной массы эволюционирующей звезды. После начала «гелиевой вспышки» звезда эволюционирует вдоль горизонтальной ветви диаграммы Герцшпрунга — Рессела. Через некоторое время после того как значительная часть гелия в ядре превратится в углерод и более тяжелые элементы, ядерные гелиевые реакции будут сосредоточены в тонком слое, окружающем уже второй раз «выгоревшее» ядро. Кроме того, у таких звезд имеется еще один наружный слой, в котором происходят водородные ядерные реакции. Звезды с такими «двухслойными» источниками ядерной энергии (схема структуры такой звезды изображена на рис. 13.5) значительно увеличивают свою светимость, которая достигает порядка нескольких тысяч светимостей Солнца, в то время как на горизонтальной ветви светимость только в сотню раз превышала солнечную. Структура таких звезд, у которых в самых центральных «выгоревших» частях никаких ядерных реакций больше не происходит, должна напоминать структуру красных гигантов. Это означает, что звезда опять «раздувается» и ее радиус доходит до размеров земной орбиты, в то время как радиус зоны «горения» водорода всего лишь порядка 3
и почти не зависит от полной массы эволюционирующей звезды. После начала «гелиевой вспышки» звезда эволюционирует вдоль горизонтальной ветви диаграммы Герцшпрунга — Рессела. Через некоторое время после того как значительная часть гелия в ядре превратится в углерод и более тяжелые элементы, ядерные гелиевые реакции будут сосредоточены в тонком слое, окружающем уже второй раз «выгоревшее» ядро. Кроме того, у таких звезд имеется еще один наружный слой, в котором происходят водородные ядерные реакции. Звезды с такими «двухслойными» источниками ядерной энергии (схема структуры такой звезды изображена на рис. 13.5) значительно увеличивают свою светимость, которая достигает порядка нескольких тысяч светимостей Солнца, в то время как на горизонтальной ветви светимость только в сотню раз превышала солнечную. Структура таких звезд, у которых в самых центральных «выгоревших» частях никаких ядерных реакций больше не происходит, должна напоминать структуру красных гигантов. Это означает, что звезда опять «раздувается» и ее радиус доходит до размеров земной орбиты, в то время как радиус зоны «горения» водорода всего лишь порядка 3  109 см. К концу этой фазы эволюции звезда опять становится красным гигантом. Ее светимость может в десятки тысяч раз превосходить солнечную, а масса тонкого гелиевого слоя в ее недрах не превосходит нескольких сотых солнечной. Зона «горения» водорода значительно поднимается наружу, так что область внутри этой оболочки уже содержит
109 см. К концу этой фазы эволюции звезда опять становится красным гигантом. Ее светимость может в десятки тысяч раз превосходить солнечную, а масса тонкого гелиевого слоя в ее недрах не превосходит нескольких сотых солнечной. Зона «горения» водорода значительно поднимается наружу, так что область внутри этой оболочки уже содержит  70% массы звезды. Вся эта фаза эволюции с двумя слоями ядерного энерговыделения занимает время порядка миллиона лет. На самых заключительных этапах этой фазы звезда уже вполне «подготовлена», чтобы от нее отошла наружная, богатая водородом оболочка и тем самым образовалась бы планетарная туманность плюс ядро. В самом деле, светимость молодых ядер планетарных туманностей в 104 раза больше солнечной и практически совпадает со светимостью «двухслойной» гигантской звезды. Радиусы, структура и массы ядер практически совпадают с радиусом, структурой и массой этой звезды под слоем «горения» водорода (т. е. «инертной», состоящей из тяжелых элементов центральной части, покрытой тонкой гелиевой «корочкой»), следовательно, будущее ядро планетарной туманности уже «сварилось» в недрах сильно проэволюционировавшей звезды. Остается только понять механизм отделения протяженной наружной, богатой водородом оболочки.
70% массы звезды. Вся эта фаза эволюции с двумя слоями ядерного энерговыделения занимает время порядка миллиона лет. На самых заключительных этапах этой фазы звезда уже вполне «подготовлена», чтобы от нее отошла наружная, богатая водородом оболочка и тем самым образовалась бы планетарная туманность плюс ядро. В самом деле, светимость молодых ядер планетарных туманностей в 104 раза больше солнечной и практически совпадает со светимостью «двухслойной» гигантской звезды. Радиусы, структура и массы ядер практически совпадают с радиусом, структурой и массой этой звезды под слоем «горения» водорода (т. е. «инертной», состоящей из тяжелых элементов центральной части, покрытой тонкой гелиевой «корочкой»), следовательно, будущее ядро планетарной туманности уже «сварилось» в недрах сильно проэволюционировавшей звезды. Остается только понять механизм отделения протяженной наружной, богатой водородом оболочки.  , найдем что «отрыв» произошел на расстоянии около одной астрономической единицы (1,5
, найдем что «отрыв» произошел на расстоянии около одной астрономической единицы (1,5  1013 см) от центра звезды, что как раз соответствует радиусу гигантской звезды — «предка» туманности. Хотя количественной теории «отрыва» оболочки у протяженной сильно проэволюционировавшей звезды пока еще нет (это очень трудная задача!), можно указать по крайней мере на три причины этого явления: а) Из-за особого характера неустойчивости в протяженной оболочке должны возникать сильные колебательные процессы, сопровождаемые изменениями теплового режима звезды. Период таких колебаний порядка десяти тысяч лет. б) Из-за ионизации водорода в некоторой зоне звезды под ее фотосферой может развиться сильная конвективная неустойчивость. Аналогичное явление имеет место на Солнце и служит первопричиной его активности. У холодных гигантских звезд мощность конвективных движений может быть несравненно больше, чем на Солнце. в) Из-за огромной светимости звезды — предка планетарной туманности — световое давление ее потока излучения на наружные слои может привести к их «сбросу». Расчеты, которые мы здесь привести не можем, показывают, что под воздействием светового давления вещество оболочки будет вытекать, причем мощность этого потока может достигнуть 1021—1022 г/с. Это означает, что за несколько тысяч лет может «истечь» практически вся оболочка звезды, что приведет к образованию планетарной туманности. Скорее всего, в действительности действуют все три механизма сброса оболочки, как бы «помогая» друг другу.
1013 см) от центра звезды, что как раз соответствует радиусу гигантской звезды — «предка» туманности. Хотя количественной теории «отрыва» оболочки у протяженной сильно проэволюционировавшей звезды пока еще нет (это очень трудная задача!), можно указать по крайней мере на три причины этого явления: а) Из-за особого характера неустойчивости в протяженной оболочке должны возникать сильные колебательные процессы, сопровождаемые изменениями теплового режима звезды. Период таких колебаний порядка десяти тысяч лет. б) Из-за ионизации водорода в некоторой зоне звезды под ее фотосферой может развиться сильная конвективная неустойчивость. Аналогичное явление имеет место на Солнце и служит первопричиной его активности. У холодных гигантских звезд мощность конвективных движений может быть несравненно больше, чем на Солнце. в) Из-за огромной светимости звезды — предка планетарной туманности — световое давление ее потока излучения на наружные слои может привести к их «сбросу». Расчеты, которые мы здесь привести не можем, показывают, что под воздействием светового давления вещество оболочки будет вытекать, причем мощность этого потока может достигнуть 1021—1022 г/с. Это означает, что за несколько тысяч лет может «истечь» практически вся оболочка звезды, что приведет к образованию планетарной туманности. Скорее всего, в действительности действуют все три механизма сброса оболочки, как бы «помогая» друг другу. 
 = 21 см. Видны две линии поглощения, соответствующие лучевым скоростям -40 км/с и +6 км/с. Стрелка указывает на скорость расширения этой туманности, полученную из наблюдений оптических линий [N II]. Внизу — такой же радиоспектр «источника сравнения» — яркой компактной области Н II XGC 6334, находящейся в двух градусах от NGC 6302. Видна только линия +6 км/с, принадлежащая (как и у NGC 6302) межзвездной среде.
= 21 см. Видны две линии поглощения, соответствующие лучевым скоростям -40 км/с и +6 км/с. Стрелка указывает на скорость расширения этой туманности, полученную из наблюдений оптических линий [N II]. Внизу — такой же радиоспектр «источника сравнения» — яркой компактной области Н II XGC 6334, находящейся в двух градусах от NGC 6302. Видна только линия +6 км/с, принадлежащая (как и у NGC 6302) межзвездной среде. = 2,64 мм — см. § 3) от инфракрасных объектов CRL 2688 и CRL 618. Анализ этой линии излучения позволяет сделать вывод, что в этих случаях наблюдаются довольно плотные газовые оболочки, расширяющиеся со скоростью
= 2,64 мм — см. § 3) от инфракрасных объектов CRL 2688 и CRL 618. Анализ этой линии излучения позволяет сделать вывод, что в этих случаях наблюдаются довольно плотные газовые оболочки, расширяющиеся со скоростью  20 км/с. Отсюда следует, что наблюдаемые в центральных частях этих объектов довольно горячие звезды стали «проглядывать» через соответствующие оболочки только несколько тысяч лет тому назад. В ту эпоху эти объекты должны были быть тождественны красным гигантам, атмосферы которых богаты углеродом. Но это как раз и означает, что объекты CRL 2688 и CRL 618 являются протопланетарными туманностями. Совсем недавно (1982 г.) на величайшем в мире радиотелескопе VLA было впервые обнаружено поглощение на волне 21 см нейтрального водорода сравнительно молодой, яркой планетарной туманности NGC 6302. Эти наблюдения выявили две компоненты линии поглощения, соответствующие лучевым скоростям +6 и -40 км/с (см. рис. 13.6). Первая компонента вызвана поглощением облака межзвездного водорода, находящегося между ними и планетарной туманностью, между тем как линия -40 км/с образуется в наружных слоях этой туманности, обращенных к наблюдателю. Из анализа этих наблюдений можно сделать вывод, что эти наружные слои представляют собой расширяющееся со скоростью 10 км/с кольцо, в то время как внутренняя часть этого кольца состоит из горячего, полностью ионизованного газа. На рис. 13.7 приведена схема строения этой туманности на основе описанных выше радиоастрономических наблюдений. Масса наружной части кольца, состоящей из нейтрального, сравнительно холодного водорода, около 0,06M
20 км/с. Отсюда следует, что наблюдаемые в центральных частях этих объектов довольно горячие звезды стали «проглядывать» через соответствующие оболочки только несколько тысяч лет тому назад. В ту эпоху эти объекты должны были быть тождественны красным гигантам, атмосферы которых богаты углеродом. Но это как раз и означает, что объекты CRL 2688 и CRL 618 являются протопланетарными туманностями. Совсем недавно (1982 г.) на величайшем в мире радиотелескопе VLA было впервые обнаружено поглощение на волне 21 см нейтрального водорода сравнительно молодой, яркой планетарной туманности NGC 6302. Эти наблюдения выявили две компоненты линии поглощения, соответствующие лучевым скоростям +6 и -40 км/с (см. рис. 13.6). Первая компонента вызвана поглощением облака межзвездного водорода, находящегося между ними и планетарной туманностью, между тем как линия -40 км/с образуется в наружных слоях этой туманности, обращенных к наблюдателю. Из анализа этих наблюдений можно сделать вывод, что эти наружные слои представляют собой расширяющееся со скоростью 10 км/с кольцо, в то время как внутренняя часть этого кольца состоит из горячего, полностью ионизованного газа. На рис. 13.7 приведена схема строения этой туманности на основе описанных выше радиоастрономических наблюдений. Масса наружной части кольца, состоящей из нейтрального, сравнительно холодного водорода, около 0,06M . Таким образом, спустя 25 лет, наша модель планетарной туманности получила полное экспериментальное подтверждение. По мере расширения туманности размеры ее наружной нейтральной части будут довольно быстро сокращаться, пока она не исчезнет совсем.
. Таким образом, спустя 25 лет, наша модель планетарной туманности получила полное экспериментальное подтверждение. По мере расширения туманности размеры ее наружной нейтральной части будут довольно быстро сокращаться, пока она не исчезнет совсем. 
 105 К) белыми карликами. Пока таких объектов известно 4. Скорее всего — это ядра планетарных туманностей, у которых оболочки вследствие расширения имеют ничтожно малую поверхностную яркость. Было бы интересно, с одной стороны, обнаружить оптические «следы» планетарных туманностей около таких объектов, а с другой стороны, попытаться измерить поток мягкого рентгеновского излучения от ближайших планетарных туманностей, например NGC 7293, фотография которой приведена на рис. 13.1 вверху.
105 К) белыми карликами. Пока таких объектов известно 4. Скорее всего — это ядра планетарных туманностей, у которых оболочки вследствие расширения имеют ничтожно малую поверхностную яркость. Было бы интересно, с одной стороны, обнаружить оптические «следы» планетарных туманностей около таких объектов, а с другой стороны, попытаться измерить поток мягкого рентгеновского излучения от ближайших планетарных туманностей, например NGC 7293, фотография которой приведена на рис. 13.1 вверху. 


 было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша.
было меньше 0,03. Это означает, что на стадии эволюции, когда масса перетекает от одной компоненты ко второй, радиус эволюционирующей звезды должен все время оставаться очень близким к радиусу полости Роша. 



 Лиры. К концу этого бурного периода в эволюции двойной системы отношение масс обеих компонент становится обратным. Если вначале, например, эволюционирующая компонента системы была вдвое массивнее второй компоненты, то к концу этого периода она станет вдвое менее массивной.
Лиры. К концу этого бурного периода в эволюции двойной системы отношение масс обеих компонент становится обратным. Если вначале, например, эволюционирующая компонента системы была вдвое массивнее второй компоненты, то к концу этого периода она станет вдвое менее массивной. 
 Лиры.
Лиры.
 ), в то время как температуры их поверхностей близки к 5000 К. Совершенно неожиданно было обнаружено, что все эти звезды показывают строго периодические изменения блеска с амплитудой около 0,01 звездной величины и с периодами в пределах от четверти до одних суток. Одновременные спектральные наблюдения некоторых из этих звезд, выполненные на большом 3-метровом рефлекторе Ликской обсерватории, позволили прийти к однозначному выводу, что причиной строго периодических вариаций блеска звезд в Плеядах является их осевое вращение. Одно полушарие звезды, как оказывается, немного более ярко, чем другое, что и объясняет периодические изменения блеска при вращении звезд.
), в то время как температуры их поверхностей близки к 5000 К. Совершенно неожиданно было обнаружено, что все эти звезды показывают строго периодические изменения блеска с амплитудой около 0,01 звездной величины и с периодами в пределах от четверти до одних суток. Одновременные спектральные наблюдения некоторых из этих звезд, выполненные на большом 3-метровом рефлекторе Ликской обсерватории, позволили прийти к однозначному выводу, что причиной строго периодических вариаций блеска звезд в Плеядах является их осевое вращение. Одно полушарие звезды, как оказывается, немного более ярко, чем другое, что и объясняет периодические изменения блеска при вращении звезд.